가우시안 소거법 (Gaussian Elimination)와 가우스-조던 소거법
선형 대수학의 핵심 알고리즘인 가우시안 소거법은 선형 방정식 시스템을 풀거나 행렬의 역행렬, 행렬식, 그리고 행렬의 계수(rank)를 계산하는 데 널리 사용됩니다. 이 방법은 독일의 수학자 카를 프리드리히 가우스(Carl Friedrich Gauss)의 이름을 따서 명명되었으며, 연립 방정식을 행 사다리꼴(Row Echelon Form) 또는 기약 행 사다리꼴(Reduced Row Echelon Form)로 변환하는 것을 목표로 합니다.
https://www.youtube.com/watch?v=L9fTll_vOxQ&pp=ygUT6rCA7Jqw7IqkIOyGjOqxsOuylQ%3D%3D
https://www.youtube.com/watch?v=Q1zCibRtI2A&pp=ygUT6rCA7Jqw7IqkIOyGjOqxsOuylQ%3D%3D
1. 기본 개념
가우시안 소거법은 행렬을 세 가지 기본 행 연산을 사용하여 변환합니다:
- 행 교환 (Row Swapping): 두 행의 순서를 바꿉니다.
- 행 스케일링 (Row Scaling): 한 행의 모든 원소를 0이 아닌 상수로 곱하거나 나눕니다.
- 행 덧셈 (Row Addition): 한 행에 다른 행의 상수 배를 더합니다.
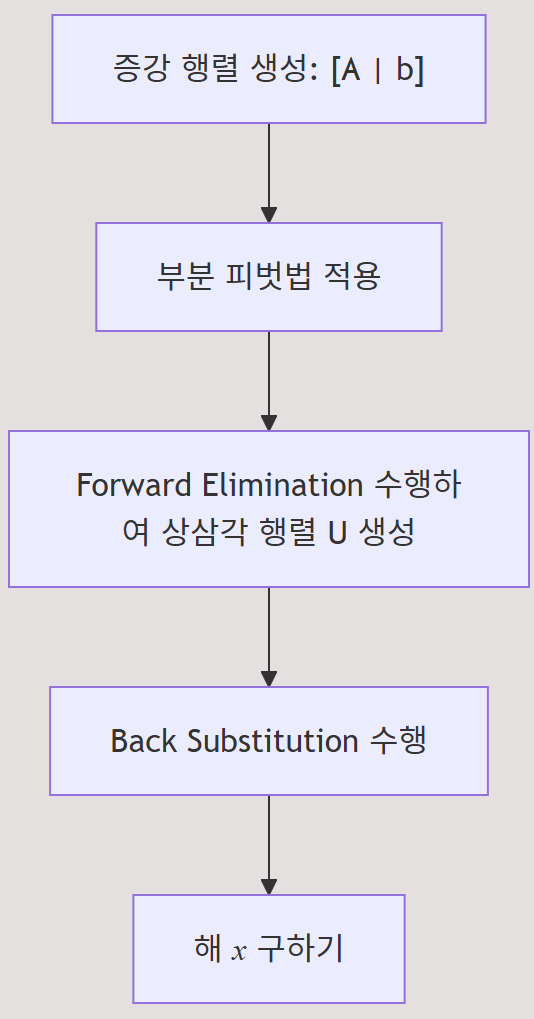
이러한 연산을 통해 증강 행렬 [A | b]를 상삼각행렬(upper triangular matrix) 또는 계단형 행렬(row echelon form)로 변환하면, 역순 대입(Back Substitution)을 통해 해를 구할 수 있게 됩니다.
주요 목표: 연립 방정식을 아래와 같이 변환하여 미지수의 값을 쉽게 구하는 것입니다.
$$ \begin{cases} a_{11}x_1 + a_{12}x_2 + \ldots + a_{1n}x_n = b_1 \\ 0\cdot x_1 + a_{22}x_2 + \ldots + a_{2n}x_n = b_2 \\ \vdots \\ 0\cdot x_1 + 0\cdot x_2 + \ldots + a_{nn}x_n = b_n \end{cases} $$2. 알고리즘 단계
2.1 Forward Elimination (전진 소거)
첫 번째 단계에서는 증강 행렬의 각 열에서 피벗(pivot)을 선택하여, 해당 열 아래의 모든 원소들을 0으로 만듭니다. 피벗 선택 시 수치적 안정성을 위해 절댓값이 가장 큰 원소를 선택하는 부분 피벗법을 사용합니다.
for k = 1 to n-1:
// k번째 열의 피벗 선택 (부분 피벗법)
max_index = index of max(|A[i][k]|) for i = k to n
if max_index ≠ k:
swap rows k and max_index
// 피벗 아래 행의 원소 소거
for i = k+1 to n:
factor = A[i][k] / A[k][k]
for j = k to n:
A[i][j] = A[i][j] - factor * A[k][j]
b[i] = b[i] - factor * b[k]
이 과정을 거치면 증강 행렬은 상삼각 행렬 \(U\)의 형태를 갖추게 됩니다.
2.2 Back Substitution (역순 대입)
상삼각 행렬이 완성되면, 마지막 행부터 시작하여 하나씩 미지수를 구합니다.
x[n] = b[n] / A[n][n]
for i = n-1 downto 1:
sum = 0
for j = i+1 to n:
sum += A[i][j] * x[j]
x[i] = (b[i] - sum) / A[i][i]
2.3 Gauss-Jordan Elimination (가우스-조던 소거법)
가우스-조던 소거법은 가우시안 소거법을 확장하여, 변환된 행렬을 기약 행 사다리꼴(Reduced Row Echelon Form)로 만듭니다. 이 과정에서는 각 피벗을 1로 만들고, 피벗이 있는 열의 다른 모든 원소를 0으로 만듭니다.
3. 예제와 단계별 과정
3.1 2x2 연립방정식 예제
간단한 2x2 연립방정식을 통해 기본 원리를 살펴봅니다.
주어진 연립방정식:
$$ \begin{aligned} 3x + 2y &= 8, \\ x - y &= 1. \end{aligned} $$
Step 1: Forward Elimination
- 첫 번째 행의 피벗 선택: 첫 번째 행의 첫 번째 원소 \(3\)을 피벗으로 선택합니다.
- 두 번째 행 소거: 두 번째 행에서 첫 번째 행의 \(\frac{1}{3}\)배를 빼서 \(x\) 계수를 0으로 만듭니다.
결과 증강 행렬 (예시):
$$ \begin{bmatrix} 3 & 2 & | & 8 \\ 0 & \frac{4}{3} & | & \frac{5}{3} \end{bmatrix} $$Step 2: Back Substitution
- \(y = \frac{(5/3)}{(4/3)} = \frac{5}{4}\)
- \(x = \frac{8 - 2y}{3} = \frac{8 - 2\cdot(5/4)}{3} = \frac{8 - 2.5}{3} \approx 1.83\)
3.2 3x3 연립방정식 예제
3개의 미지수를 포함한 연립방정식을 통해 보다 복잡한 과정을 살펴봅니다.
주어진 연립방정식:
$$ \begin{aligned} 2x + 3y - z &= 5, \\ 4x + y + 2z &= 6, \\ -2x + 5y + 2z &= 7. \end{aligned} $$
Step 1: 증강 행렬 작성
$$ \begin{bmatrix} 2 & 3 & -1 & | & 5 \\ 4 & 1 & 2 & | & 6 \\ -2 & 5 & 2 & | & 7 \end{bmatrix} $$Step 2: Forward Elimination
- 첫 번째 행 피벗 사용: 첫 번째 행의 피벗 \(2\)를 기준으로 두 번째 행에는 \(4/2 = 2\)배, 세 번째 행에는 \(-2/2 = -1\)배를 적용하여 \(x\) 계수를 소거합니다.
- 부분 피벗 적용: 필요시 행 교환을 통해 더 큰 피벗을 선택하여 수치적 안정성을 확보합니다.
이 과정을 거치면 증강 행렬은 상삼각 행렬의 형태가 됩니다.
Step 3: Back Substitution
x[3] = b[3] / A[3][3]
x[2] = (b[2] - A[2][3]*x[3]) / A[2][2]
x[1] = (b[1] - A[1][2]*x[2] - A[1][3]*x[3]) / A[1][1]
최종적으로 \(x\), \(y\), \(z\)의 값을 구하여 연립방정식의 해를 얻습니다.
4. 응용 및 구현
4.1 역행렬 및 행렬식 계산
가우시안 소거법은 단순히 연립 방정식의 해를 구하는 데 그치지 않고, 다음과 같은 응용 분야에서도 사용됩니다:
- 역행렬 계산: 원래 행렬 \(A\)와 단위 행렬 \(I\)를 나란히 배치한 증강 행렬 \([A | I]\)에 가우스-조던 소거법을 적용하면, \(A\) 부분이 단위 행렬로 변환되고 오른쪽 부분이 \(A^{-1}\)가 됩니다.
- 행렬식 계산: 행렬을 상삼각 행렬로 변환한 후, 대각선 원소의 곱을 계산하여 행렬식을 구할 수 있습니다. 단, 행 교환이 발생하면 행렬식의 부호가 반전됨에 주의해야 합니다.
4.2 선형 방정식의 해의 존재 및 유일성 판단
증강 행렬의 계수(rank)를 분석하면 연립 방정식이 해를 가지는지, 유일한 해가 존재하는지, 또는 무수히 많은 해나 해가 없는지를 판별할 수 있습니다.

5. 구현 시 고려사항 및 복잡도
컴퓨터로 가우시안 소거법을 구현할 때는 다음 사항들을 고려해야 합니다:
- 피벗 선택: 절댓값이 가장 큰 원소를 선택하는 부분 피벗팅 또는 완전 피벗팅 기법을 사용하여 수치적 불안정성을 최소화합니다.
- 반올림 오차: 부동 소수점 연산의 특성상 발생할 수 있는 반올림 오차를 관리하기 위해 적절한 정밀도 설정이 필요합니다.
- 계산 복잡도: \(n \times n\) 행렬에 대해 가우시안 소거법은 대략 \(O(n^3)\)의 연산량을 요구하므로, 매우 큰 시스템에서는 효율적인 알고리즘 개선이나 수치 해법 기법이 필요할 수 있습니다.
6. 결론
가우시안 소거법은 선형 대수학에서 가장 기본적이고 강력한 도구로, 연립 방정식의 해 구하기, 역행렬 및 행렬식 계산, 그리고 행렬의 계수 결정 등 다양한 응용 분야에서 핵심 역할을 합니다. 알고리즘의 각 단계—피벗 선택, 전진 소거, 역순 대입(및 필요시 기약 행 사다리꼴 변환)—을 명확히 이해하고, 수치적 안정성을 확보하기 위한 피벗 전략 및 반올림 오차 관리의 중요성을 인지하는 것이 필수적입니다.
예시
다음은 두 미지수 $x$와 $y$에 대한 연립방정식
$$
\begin{cases}
2x+3y=8 \quad (1)\\[6pt]
4x+y=9 \quad (2)
\end{cases}
$$
에 대해 가우스 소거법을 적용한 예시 계산이다.
1. 첨가 행렬 작성
연립방정식을 첨가 행렬로 나타내면
$$
\left[
\begin{array}{cc|c}
2 & 3 & 8\\[4pt]
4 & 1 & 9
\end{array}
\right]
$$
이다.
2. 피봇 행 선택 및 소거
첫 번째 행의 첫 번째 원소 $2$를 피봇으로 선택한다. 두 번째 행의 $x$ 계수를 소거하기 위하여, 첫 번째 행을 2배한 후 두 번째 행에서 빼준다.
첫 번째 행을 2배하면
$$
(2\times2,\; 2\times3,\; 2\times8)=(4,\;6,\;16)
$$
이다.
두 번째 행에서 첫 번째 행의 2배를 빼면
$$
(4,\;6,\;16)-(4,\;1,\;9)=(0,\;5,\;7)
$$
로, 새로운 두 번째 행은
$$
\left[
\begin{array}{cc|c}
2 & 3 & 8\\[4pt]
0 & 5 & 7
\end{array}
\right]
$$
이다.
3. 후진 대입법
두 번째 행은
$$
5y=7
$$
이므로,
$$
y=\frac{7}{5}
$$
이다.
첫 번째 행에 $y$의 값을 대입하면
$$
2x+3\left(\frac{7}{5}\right)=8
$$
이다. 양변에서 $3\times\frac{7}{5}=\frac{21}{5}$를 빼면
$$
2x=8-\frac{21}{5}=\frac{40}{5}-\frac{21}{5}=\frac{19}{5}
$$
따라서,
$$
x=\frac{19}{10}
$$
이다.
4. 최종 해
가우스 소거법을 통해 구한 해는
$$
x=\frac{19}{10},\quad y=\frac{7}{5}
$$
이다.
다음은 세 미지수 $x$, $y$, $z$에 대한 연립방정식
$$
\begin{cases}
x + 2y + 3z = 9 \quad (1)\\
2x + 5y + 2z = 12 \quad (2)\\
3x + y + z = 8 \quad (3)
\end{cases}
$$
에 대해 가우스 소거법을 적용한 예시 계산이다.
## 1. 첨가 행렬 작성
위 연립방정식을 첨가 행렬(augmented matrix)로 나타내면 다음과 같다.
$$
\left[
\begin{array}{ccc|c}
1 & 2 & 3 & 9\\
2 & 5 & 2 & 12\\
3 & 1 & 1 & 8
\end{array}
\right]
$$
---
## 2. 가우스 소거 단계
### (1) 첫 번째 피봇: $1$ (첫 번째 행의 첫 번째 원소)
- **목표**: 아래 행들의 $x$ 계수를 0으로 만든다.
1. 두 번째 행에서 첫 번째 행의 2배를 빼기
- 첫 번째 행을 2배: $(2, 4, 6, 18)$
- 두 번째 행에서 뺀다:
$$
(2, 5, 2, 12) - (2, 4, 6, 18) = (0, 1, -4, -6)
$$
2. 세 번째 행에서 첫 번째 행의 3배를 빼기
- 첫 번째 행을 3배: $(3, 6, 9, 27)$
- 세 번째 행에서 뺀다:
$$
(3, 1, 1, 8) - (3, 6, 9, 27) = (0, -5, -8, -19)
$$
- **변환 후 행렬**:
$$
\left[
\begin{array}{ccc|c}
1 & 2 & 3 & 9\\
0 & 1 & -4 & -6\\
0 & -5 & -8 & -19
\end{array}
\right]
$$
---
### (2) 두 번째 피봇: $1$ (두 번째 행의 두 번째 원소)
- **목표**: 세 번째 행의 $y$ 계수를 0으로 만든다.
1. 세 번째 행에 (두 번째 행의 5배)를 더하기
- 두 번째 행을 5배: $(0, 5, -20, -30)$
- 세 번째 행에서 더한다:
$$
(0, -5, -8, -19) + (0, 5, -20, -30) = (0, 0, -28, -49)
$$
- **변환 후 행렬**:
$$
\left[
\begin{array}{ccc|c}
1 & 2 & 3 & 9\\
0 & 1 & -4 & -6\\
0 & 0 & -28 & -49
\end{array}
\right]
$$
---
### (3) 세 번째 피봇: $-28$ (세 번째 행의 세 번째 원소)
- 세 번째 행을 $-28$로 나누어 $z$의 계수를 1로 만든다.
$$
\frac{1}{-28}(0, 0, -28, -49) = (0, 0, 1, \tfrac{49}{28})
$$
- **변환 후 행렬**:
$$
\left[
\begin{array}{ccc|c}
1 & 2 & 3 & 9\\
0 & 1 & -4 & -6\\
0 & 0 & 1 & \frac{49}{28}
\end{array}
\right]
$$
여기서
$$
z = \frac{49}{28} = \frac{7}{4}
$$
---
## 3. 해 구하기 (후진 대입)
### (1) $z = \tfrac{7}{4}$
두 번째 행은
$$
0x + 1y - 4z = -6
$$
즉,
$$
y - 4\left(\frac{7}{4}\right) = -6 \\
y - 7 = -6 \\
y = 1
$$
### (2) $y = 1$
첫 번째 행은
$$
x + 2y + 3z = 9
$$
이므로,
$$
x + 2(1) + 3\left(\frac{7}{4}\right) = 9 \\
x + 2 + \frac{21}{4} = 9 \\
x + \frac{8}{4} + \frac{21}{4} = 9 \\
x + \frac{29}{4} = 9 \\
x = 9 - \frac{29}{4} = \frac{36}{4} - \frac{29}{4} = \frac{7}{4}
$$
---
## 4. 최종 해
$$
x = \frac{7}{4}, \quad y = 1, \quad z = \frac{7}{4}
$$
이와 같이 가우스 소거법을 통해 단계적으로 계수를 소거하고, 후진 대입법을 사용해 해를 구할 수 있다.
'Tech > Coding' 카테고리의 다른 글
| 바이트배열을 이용한 에라토스테네스의 체와 그 업그레이드 버전 (0) | 2025.03.01 |
|---|---|
| 에라스토테네스의 체 추가실험(로컬에서 실험) (0) | 2025.02.28 |
| 벨만 포드 알고리즘 (0) | 2025.02.24 |
| 에라토스테네스의 체 (0) | 2025.02.24 |
| 1836🐨트리의 가짓수 세기 .py (0) | 2025.02.23 |



