벨만 포드 알고리즘
그래프에서 최단 경로를 찾기 위한 방법 중 하나로, 음수 가중치가 포함된 경우에도 사용할 수 있다는 점에서 큰 강점.
1. 벨만 포드 알고리즘 개요
- 음수 가중치 지원: 다익스트라 알고리즘과 달리 음수 가중치 간선이 존재해도 올바른 최단 경로를 계산할 수 있습니다.
- 음수 사이클 검출: 알고리즘 수행 후, 추가적인 음수 사이클 존재 여부를 확인할 수 있습니다.
- 시간 복잡도: 일반적으로 O(VE)로, 노드(V)와 간선(E)의 수에 비례하는 시간이 소요됩니다.
벨만 포드 알고리즘은 단일 출발점 최단 경로 문제를 해결하는 데 유용하며, 특히 음수 간선을 포함한 다양한 문제에서 많이 활용됩니다.
2. 알고리즘 동작 원리
벨만 포드 알고리즘의 핵심 아이디어는 릴렉세이션(relaxation)입니다. 각 간선을 반복적으로 확인하면서, 출발지에서 도착지로 가는 경로 비용을 갱신하는 방식으로 동작합니다.
릴렉세이션 과정
- 모든 정점의 최단 경로 값을 무한대로 초기화하고, 시작 정점의 값은 0으로 설정합니다.
- 간선들을 순회하며, 현재까지 알고 있는 경로보다 더 짧은 경로가 있으면 값을 갱신합니다.
- 이 과정을 모든 정점에 대해 최대 V-1번 반복합니다.
- 추가적인 반복을 통해 값이 갱신된다면, 음수 사이클이 존재한다고 판단할 수 있습니다.
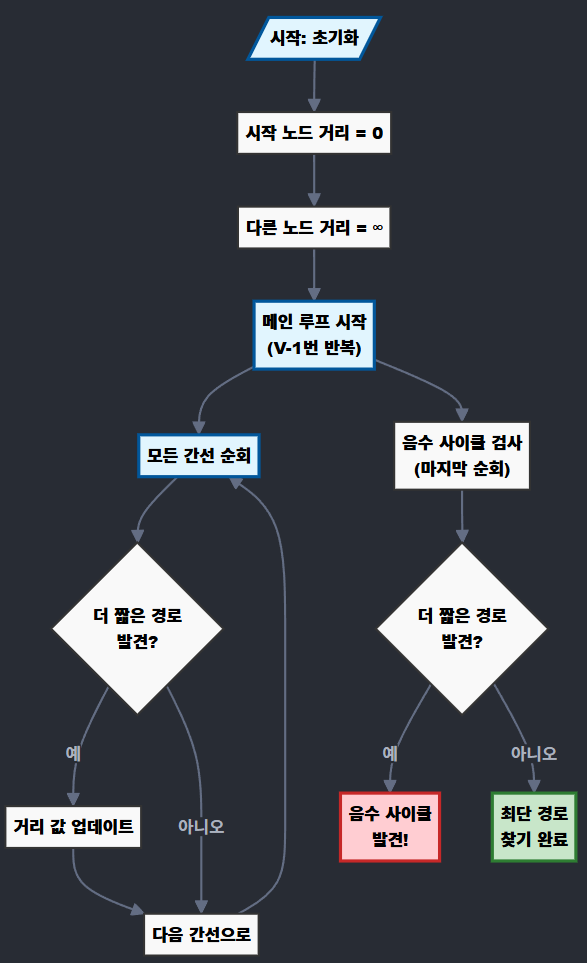
아래는 알고리즘의 간단한 의사코드입니다:
function BellmanFord(start):
// 1. 초기화
for each vertex v in graph:
distance[v] = INF
distance[start] = 0
// 2. 릴렉세이션 반복 (V-1번)
for i from 1 to V-1:
for each edge (u, v) with weight w:
if distance[u] + w < distance[v]:
distance[v] = distance[u] + w
// 3. 음수 사이클 검출
for each edge (u, v) with weight w:
if distance[u] + w < distance[v]:
return "음수 사이클 존재"
return distance
3. 구현 예제
파이썬으로 구현한 예제를 살펴보겠습니다.
def bellman_ford(graph, start):
# graph: (u, v, w) 튜플의 리스트
INF = float('inf')
distance = {vertex: INF for vertex in graph['vertices']}
distance[start] = 0
# 릴렉세이션 (V-1번 반복)
for _ in range(len(graph['vertices']) - 1):
for u, v, w in graph['edges']:
if distance[u] != INF and distance[u] + w < distance[v]:
distance[v] = distance[u] + w
# 음수 사이클 검출
for u, v, w in graph['edges']:
if distance[u] != INF and distance[u] + w < distance[v]:
return None, "음수 사이클 존재"
return distance, None
# 예제 그래프
graph = {
'vertices': ['A', 'B', 'C', 'D'],
'edges': [
('A', 'B', 1),
('B', 'C', 3),
('A', 'C', 10),
('C', 'D', 2),
('D', 'B', -6)
]
}
distances, error = bellman_ford(graph, 'A')
if error:
print(error)
else:
print("최단 경로:", distances)
4. 알고리즘 분석 및 고려사항
- 시간 복잡도: O(VE)로, 노드와 간선의 수가 많을 경우 성능이 저하될 수 있습니다.
- 음수 사이클: 음수 사이클이 존재할 경우, 최단 경로를 정의할 수 없으므로 별도의 처리가 필요합니다.
- 응용 분야: 네트워크 라우팅, 경제학에서의 최적화 문제, 그리고 다양한 경로 탐색 문제에 활용됩니다.
5. 연습문제
벨만 포드 알고리즘을 직접 구현하고 다양한 케이스에 적용해 보며 실력을 다져보세요. 아래는 백준에서 풀어볼 수 있는 문제입니다:
백준 사이트에서 "벨만 포드" 또는 "음수 사이클" 등으로 검색해 보시면 도움이 될 것입니다.
결론
벨만 포드 알고리즘은 음수 가중치를 포함한 그래프에서 최단 경로를 찾기 위한 강력한 도구입니다. 기본 개념인 릴렉세이션을 이해하고, 음수 사이클 검출 방법을 숙지하면 다양한 문제 해결에 응용할 수 있습니다.
https://www.youtube.com/watch?v=PIT-aYPPPIQ
'Tech > Coding' 카테고리의 다른 글
| 에라스토테네스의 체 추가실험(로컬에서 실험) (0) | 2025.02.28 |
|---|---|
| 가우시안 소거법 (0) | 2025.02.25 |
| 에라토스테네스의 체 (0) | 2025.02.24 |
| 1836🐨트리의 가짓수 세기 .py (0) | 2025.02.23 |
| 14939🐨불 끄기-파이썬 (0) | 2025.02.21 |



