1836번: 트리의 가짓수 세기
| 시간 제한 | 메모리 제한 |
| 2 초 | 128 MB |
문제 설명
노드의 개수 n과 트리의 높이 k가 주어질 때, 각 노드가 자식 노드를 0개 또는 2개만 갖는 완전 이진트리 중에서 높이가 정확히 k인 트리의 가짓수를 구합니다. 단, 트리의 가짓수가 매우 클 수 있으므로 최종 결과는 9901로 나눈 나머지를 출력해야 합니다.
예제 입력
5 3예제 출력
2해결 과정
이 문제는 다이나믹 프로그래밍(DP)을 활용하여 해결할 수 있습니다. 알고리즘의 핵심 포인트는 다음과 같습니다.
- 완전 이진트리의 조건: 각 노드는 자식이 0개 또는 2개여야 하므로, 전체 노드의 수 $n$은 반드시 홀수여야 합니다. 만약 $n$이 짝수라면 완전 이진트리를 구성할 수 없으므로 결과는 0입니다.



높이4 노드9개인 예






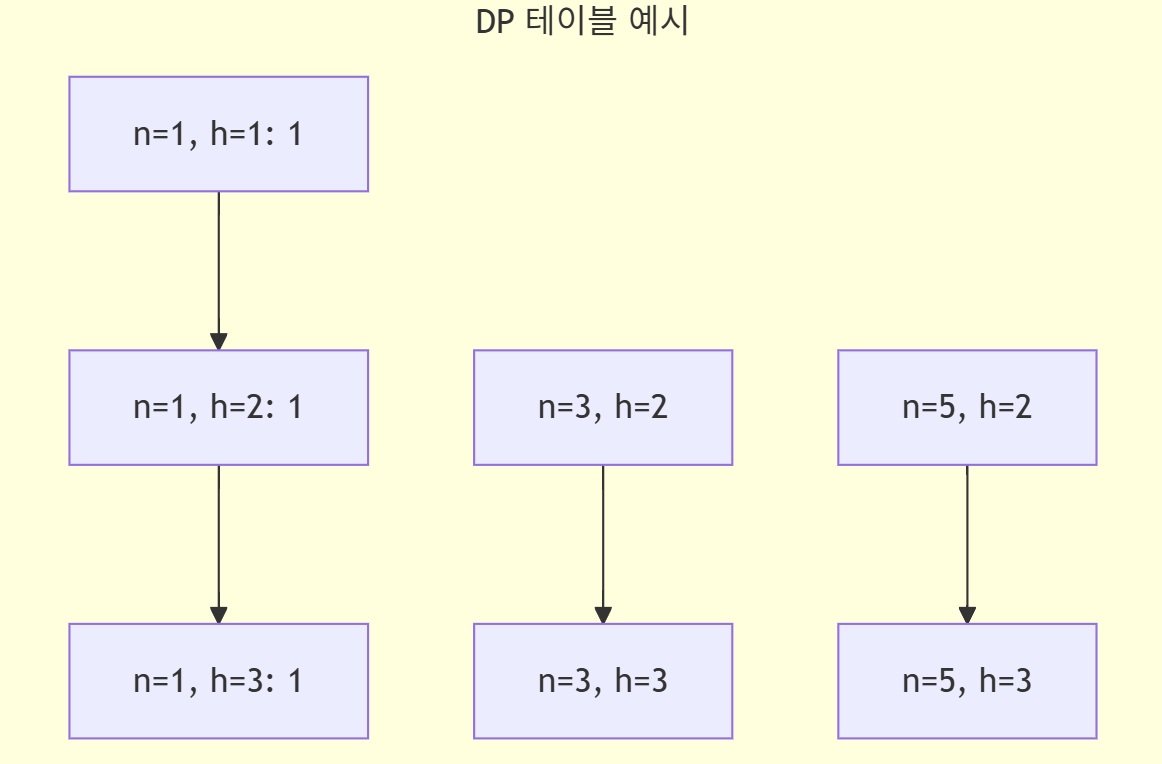
- DP 테이블 정의:
- $D(n, h)$를 노드가 $n$개이고 최대 높이가 $h$인 트리의 가짓수라고 정의합니다.
- 기본 케이스: 하나의 노드만 가진 트리는 높이에 상관없이 1가지 경우가 있습니다. 따라서 모든 $h ≥ 1$에 대해 $D(1, h)=1$로 초기화합니다.
- 재귀 관계: 노드 수가 3 이상인 경우, 트리는 루트 노드와 두 개의 서브트리(왼쪽, 오른쪽)로 구성됩니다. 만약 왼쪽 서브트리의 노드 수를 $left$라고 하면, 오른쪽 서브트리의 노드 수는 $n - 1 - left$가 됩니다. 두 서브트리의 높이가 $h-1$를 만족하는 경우의 수를 곱한 값을 더하여 전체 경우의 수를 구합니다.
예를 들어 n=5(총 노드 수)인 경우,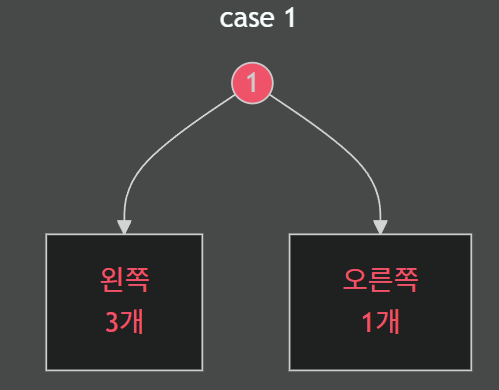

- 기본 구성
- 루트 노드가 1개 있음
- 왼쪽과 오른쪽에 서브트리가 있음
- 전체 노드 수는 5개
- 노드 분배 방법
- 루트 노드가 1개를 사용했으니 남은 노드는 4개
- 이 4개를 왼쪽과 오른쪽에 나눠야 함
- 각 노드는 반드시 0개 또는 2개의 자식을 가져야 하므로 홀수개씩 분배
- 가능한 분배:
- 왼쪽 3개, 오른쪽 1개
- 왼쪽 1개, 오른쪽 3개
- 계산 방법
- 왼쪽에 3개를 주면: 왼쪽 서브트리의 경우의 수 × 오른쪽 서브트리(1개)의 경우의 수
- 왼쪽에 1개를 주면: 왼쪽 서브트리(1개)의 경우의 수 × 오른쪽 서브트리(3개)의 경우의 수
- 이 두 경우를 더하면 전체 경우의 수가 됨
- 전체 노드 수(n)에서
- 루트 노드(1)를 빼고
- 왼쪽에 준 노드 수(left)를 빼면
- 오른쪽에 줄 수 있는 노드 수가 됨
- 기본 구성
- 정확한 높이 계산: DP 테이블 $D(n, k)$는 최대 높이가 $k$인 트리의 개수를 포함합니다. 따라서 높이가 정확히 $k$인 트리의 가짓수는 $D(n, k) - D(n, k-1)$로 계산할 수 있습니다.

파이썬 코드
def sol():
MOD = 9901
n, k = map(int, open(0).read().split())
if n & 1 == 0: # full binary tree는 n이 홀수
print(0)
return
# D[n][h] : 노드가 n개, 최대 높이 h인 트리의 가짓수
D = [[0] * (k + 1) for _ in range(n + 1)]
# 1개의 노드를 가진 트리는 어떤 높이에서도 1가지 경우가 있음.
for height in range(1, k + 1):
D[1][height] = 1
# 노드 수가 3 이상인 경우 (홀수만 고려)
for nodes in range(3, n + 1, 2):
for height in range(2, k + 1):
D[nodes][height] = 0
# 왼쪽 서브트리의 노드 개수를 left, 오른쪽 서브트리의 노드 개수는 nodes - 1 - left
for left in range(1, nodes, 2):
right = nodes - 1 - left
D[nodes][height] = (D[nodes][height] + D[left][height - 1] * D[right][height - 1]) % MOD
# 높이가 정확히 k인 트리의 개수 = D[n][k] - D[n][k-1]
result = (D[n][k] - D[n][k - 1]) % MOD
print(result)
sol()코드 설명
1. n과 k를 입력받습니다. 만약 n이 짝수라면 완전 이진트리 조건에 부합하지 않으므로 0을 출력하고 종료합니다.
2. DP 테이블 D를 (n+1) x (k+1) 크기로 초기화합니다. 각 원소 D[n][h]는 노드가 n개이고 최대 높이가 h인 트리의 가짓수를 의미합니다.
3. 기본 케이스로, 1개의 노드를 가진 트리는 어떤 높이에서도 1가지 경우가 있으므로, 모든 height에 대해 D[1][height]=1로 설정합니다.
4. 노드 수가 3 이상인 경우, 루트 노드 하나와 두 서브트리로 구성되므로, 왼쪽 서브트리의 노드 수를 left라 할 때 오른쪽 서브트리의 노드 수는 nodes - 1 - left가 됩니다. 두 서브트리 모두 높이가 height-1를 만족하는 경우의 수를 곱해 전체 경우의 수에 더합니다.
5. 최종적으로, DP 테이블 D[n][k]는 최대 높이가 k인 트리의 개수를 포함하므로, 정확히 높이가 k인 트리의 경우의 수는 D[n][k] - D[n][k-1]로 계산됩니다.

'Tech > Coding' 카테고리의 다른 글
| 벨만 포드 알고리즘 (0) | 2025.02.24 |
|---|---|
| 에라토스테네스의 체 (0) | 2025.02.24 |
| 14939🐨불 끄기-파이썬 (0) | 2025.02.21 |
| 이분그래프 (0) | 2025.02.19 |
| 해결한 문제 간단 리뷰(2.8~2.13) (0) | 2025.02.13 |



