def lcs(A, B):
lenA, lenB = len(A), len(B)
DP = [[0] * (lenB+1) for _ in range(lenA+1)]
for i in range(1, lenA+1):
for j in range(1, lenB+1):
if A[i-1] == B[j-1]:
DP[i][j] = DP[i-1][j-1] + 1
else:
DP[i][j] = max(DP[i-1][j], DP[i][j-1])
return DP[lenA][lenB]
def main():
A = input()
B = input()
print(lcs(A, B))
if __name__ == "__main__":
main()- lcs(A, B) 함수는 두 문자열 A와 B를 입력으로 받습니다.
- 변수 lenA와 lenB는 각각 문자열 A와 B의 길이를 저장합니다.
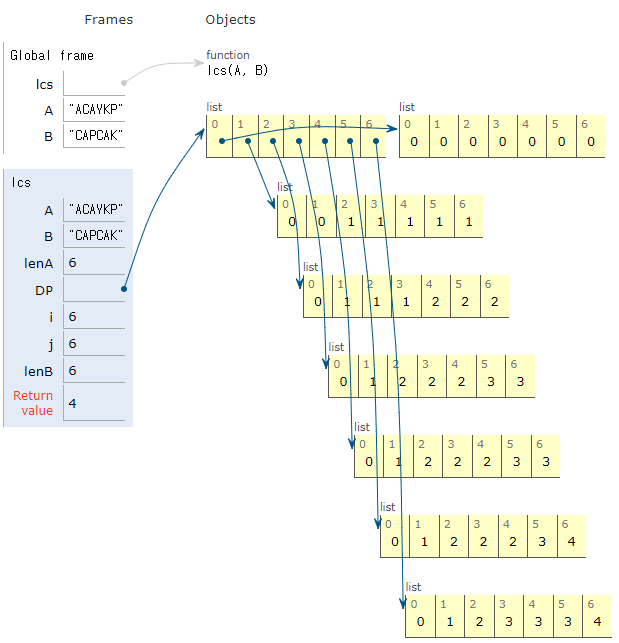
- DP는 동적 프로그래밍을 위한 2차원 리스트로, 크기는 (lenA+1) x (lenB+1)입니다. 모든 요소는 0으로 초기화됩니다.
- 이중 for 반복문을 사용하여 A와 B의 각 문자를 순회하며, 현재 위치에서의 LCS 길이를 계산합니다.
- 만약 A의 i번째 문자와 B의 j번째 문자가 같다면, DP[i][j]는 DP[i-1][j-1] + 1로 업데이트됩니다. 이는 이전 위치의 LCS 길이에 현재 일치하는 문자를 추가하는 것을 의미합니다.
- 문자가 일치하지 않는 경우, DP[i][j]는 max(DP[i-1][j], DP[i][j-1])로 업데이트됩니다. 즉, 이전 단계에서의 최대 LCS 길이를 유지합니다.
- 마지막으로 DP[lenA][lenB]는 두 문자열 A와 B의 LCS 길이를 나타냅니다.
def lcs_optimized(A, B):
if len(B) > len(A):
A, B = B, A # A가 더 긴 문자열이 되도록 함
lenA, lenB = len(A), len(B)
prev = [0] * (lenB + 1)
for i in range(1, lenA + 1):
current = [0]
for j in range(1, lenB + 1):
if A[i - 1] == B[j - 1]:
current.append(prev[j - 1] + 1)
else:
current.append(max(prev[j], current[-1]))
prev = current
return prev[-1]
def main():
A = input("첫 번째 문자열을 입력하세요: ")
B = input("두 번째 문자열을 입력하세요: ")
print(lcs_optimized(A, B))
if __name__ == "__main__":
main()메모리 사용 최적화
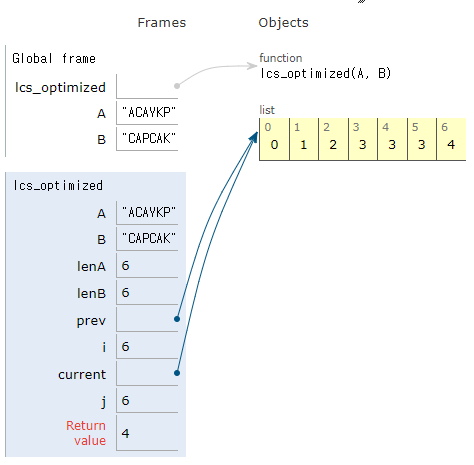
현재 구현에서는 lenA+1 행과 lenB+1 열의 2차원 배열을 사용하고 있습니다. 각 셀 DP[i][j]는 A[0..i]와 B[0..j] 사이의 LCS의 길이를 저장합니다. 하지만 각 단계에서 이전 행만 참조하기 때문에 전체 행을 저장할 필요가 없습니다. 따라서 메모리 사용을 최적화하기 위해 2개의 배열만 사용할 수 있습니다.
코드 최적화
메모리 사용 최적화: LCS 계산 시, 전체 행렬 대신 현재 행과 이전 행만 저장하는 방식으로 메모리 사용량을 줄일 수 있습니다. 이렇게 하면 공간 복잡도를 O(min(lenA, lenB))로 줄일 수 있습니다.
'Tech > Coding' 카테고리의 다른 글
| 카데인 알고리즘(Kadane's Algorithm) (0) | 2024.02.24 |
|---|---|
| RGB거리 (0) | 2024.02.22 |
| # 12865 평범한 배낭(Python 파이썬) (0) | 2024.02.17 |
| 백트래킹(Backtracking, 퇴각검색) # 14889번 스타트와 링크, # 9663번 N-Queen [파이썬] (0) | 2024.02.14 |
| 프로필 마크다운 (0) | 2024.02.10 |



