이동
| 시간 제한 | 메모리 제한 |
|---|---|
| 1 초 | 512 MB |
문제
$N$개의 수가 있는 $X$와 $Y$가 있다. 이때 $X$나 $Y$를 순환 이동시킬 수 있다. 순환 이동이란 마지막 원소를 제거하고 그 수를 맨 앞으로 다시 삽입하는 것을 말한다. 예를 들어, ${1, 2, 3}$을 순환 이동시키면 ${3, 1, 2}$가 될 것이고, ${3, 1, 2}$는 ${2, 3, 1}$이 된다. 순환 이동은 $0$번 또는 그 이상 할 수 있다. 이 모든 순환 이동을 한 후에 점수를 구하면 된다. 점수 $S$는 다음과 같이 구한다.
$$S = X[0]×Y[0] + X[1]×Y[1] + ... + X[N-1]×Y[N-1]$$
이때 $S$를 최대로 하면 된다.
입력
첫째 줄에 $N$이 주어진다. 둘째 줄에는 $X$에 들어있는 $N$개의 수가 주어진다. 셋째 줄에는 $Y$에 있는 수가 모두 주어진다. $N$은 $60,000$보다 작거나 같은 자연수이고, $X$와 $Y$에 들어있는 모든 수는 $100$보다 작은 자연수 또는 $0$이다.
출력
첫째 줄에 $S$의 최댓값을 출력한다.
예제 입력 1
4
1 2 3 4
6 7 8 5예제 출력 1
70예제 입력 2
5
1 1 1 1 1
1 1 1 1 1예제 출력 2
5예제 입력 3
10
23 4 95 20 17 94 63 44 13 96
87 54 13 18 61 24 17 94 53 2예제 출력 3
28886✨ 문제 요약
두 수열 X, Y가 있을 때, 하나를 원형으로 돌려가며(순환 이동) 곱한 점수의 최댓값을 구하는 문제입니다. 예를 들어:
복사
X = [1, 2, 3] Y = [4, 5, 6]
X를 돌려가며 곱하면:
- $X$ 그대로: $1×4 + 2×5 + 3×6 = 32$
- $X$ 회전 1번: $3×4 + 1×5 + 2×6 = 29$
- $X$ 회전 2번: $2×4 + 3×5 + 1×6 = 29$
최댓값은 $32$입니다. 이를 효율적으로 계산하는 방법을 알아봅시다.
📌 1. 내적(dot product)이란?
내적은 두 수열을 곱하고 더하는 작업입니다.
일상적인 예로 설명하자면:
당신이 하루에 각각 3시간, 2시간, 4시간을 공부했고, 그날의 집중력 점수가 각각 80, 60, 90이었다면?
전체 효율은 이렇게 계산합니다: $3×80 + 2×60 + 4×90 = 240 + 120 + 360 = 720$
즉, 내적은:
- 같은 위치의 숫자를 곱한 후
- 전부 더하는 것입니다.
🔁 2. 순환 이동(Circular Shift)이란?
수열을 끝에서 앞으로 돌리는 작업입니다:
복사
[1, 2, 3] → [3, 1, 2] → [2, 3, 1] → [1, 2, 3] (원래대로)
마치 회전하는 벨트처럼 계속 돌 수 있습니다.
🧩 3. 순환 이동 내적의 최댓값 구하기
문제는 다음과 같습니다:
- X를 계속 돌려가며
- Y와 내적을 계속 계산
- 그 중 최댓값을 찾기
하지만 X, Y가 최대 6만 개라면 하나씩 다 계산하면 $60,000 × 60,000$으로 시간 초과가 발생합니다.
🔀 4. 컨볼루션(합성곱, convolution) 쉽게 이해하기
📦 비유: 포장 작업
물건을 포장하는 작업장을 상상해보세요:
- 왼쪽 벨트에는 상자들이 줄 서 있고
- 오른쪽 벨트에는 스티커가 줄 서 있습니다
두 벨트를 맞대고 각 상자에 스티커를 붙입니다. 그날의 포장 효율은 상자와 스티커의 품질을 곱하고 다 더한 값입니다. 오른쪽 벨트를 한 칸씩 밀어보면 새로운 조합이 생기고, 그때마다 새로운 효율이 계산됩니다.
이렇게 한 벨트를 움직이면서 곱한 후 더하는 작업을 컴퓨터 과학에서는 컨볼루션(합성곱)이라고 부릅니다.
⚡ 5. 빠른 컨볼루션 = FFT
📈 문제: 연산량이 너무 많다
모든 위치에서 곱하고 더하려면 O(N²) 시간이 걸려 현실적으로 불가능합니다. 그래서 등장한 것이 FFT(Fast Fourier Transform)입니다.
🧠 6. Cooley-Tukey FFT: 쉽게 설명하기
📻 비유: 라디오 주파수 해석
음악을 분석할 때, 소리를 주파수로 나눠서 본다고 생각해보세요. 예를 들어 어떤 음악에 도 음이 많은지, 미 음이 많은지를 계산하려면 전체 소리를 작은 파형(기본 주파수)으로 분해해야 합니다.
FFT는 바로 이런 일을 하는 도구입니다.
🧪 FFT를 이용한 컨볼루션 계산 과정
- 수열을 주파수 형태로 바꿈 (FFT)
- 주파수 영역에서 각각 곱함 (이 단계에서 곱셈은 쉽게 끝남)
- 다시 원래 수열로 복구 (역 FFT)
⚙ 실제 계산 예시
- A = [1, 2, 3]
- B = [4, 5, 6]
이 두 수열의 합성곱은:
복사
1×4 = 4 1×5 + 2×4 = 5 + 8 = 13 1×6 + 2×5 + 3×4 = 6 + 10 + 12 = 28 2×6 + 3×5 = 12 + 15 = 27 3×6 = 18
결과 = [4, 13, 28, 27, 18]
이를 하나하나 계산하면 오래 걸리지만, FFT를 사용하면 O(N log N) 시간에 가능하므로 훨씬 빠릅니다.
🔄 FFT 변환이란?
시간 영역(Time Domain)의 수열을 주파수 영역(Frequency Domain)으로 바꾸는 방법입니다.
수열을 구성하는 주기적인 패턴(진동 성분)을 분석할 수 있게 도와줍니다.
📘 수학적 정의: DFT
길이 \( N \)의 수열 \( x_0, x_1, ..., x_{N-1} \) 에 대해
이산 푸리에 변환(DFT) 은 다음과 같이 정의됩니다:
$$Xk=∑n=0N−1xn⋅e−2πi⋅kn/N,(k=0,1,...,N−1)X_k = \sum_{n=0}^{N-1} x_n \cdot e^{-2\pi i \cdot kn/N},\quad (k = 0, 1, ..., N-1)
여기서 복소수 지수는 사인/코사인 파형을 의미합니다 (오일러 공식)
🧠 핵심 아이디어
DFT의 직관:
- 입력 수열을 사인/코사인 주파수로 분해
- 각 주파수가 입력에 얼마나 섞여 있는지를 계수로 나타냄
문제점:
- DFT는 직접 계산하면 O(N²) 이 걸림
해결책:
- FFT(Fast Fourier Transform) 는 같은 결과를 O(N log N) 으로 빠르게 계산
🧮 간단한 예시: 길이 4 수열
입력: $ x = [a, b, c, d] \) (길이 \( N=4 \)$
복소수 유닛 루트:
W40=1W41=iW42=−1W43=−i\begin{align*} W_4^0 &= 1\\ W_4^1 &= i\\ W_4^2 &= -1\\ W_4^3 &= -i\\ \end{align*}
DFT 직접 계산
X0=a+b+c+dX1=a+bW41+cW42+dW43X2=a+bW42+cW44+dW46X3=a+bW43+cW46+dW49\begin{align*} X_0 &= a + b + c + d\\ X_1 &= a + bW_4^1 + cW_4^2 + dW_4^3\\ X_2 &= a + bW_4^2 + cW_4^4 + dW_4^6\\ X_3 &= a + bW_4^3 + cW_4^6 + dW_4^9\\ \end{align*}
→ 복소수 곱셈 16번 필요
⚡ Cooley–Tukey FFT 알고리즘
FFT는 DFT(이산 푸리에 변환)를 다음 방식으로 분할 정복(Divide & Conquer) 합니다:
- 입력을 짝수/홀수 인덱스로 분리:
- 원래 수열 x[0],x[1],...,x[N−1]x[0], x[1], ..., x[N-1]을 두 부분으로 나눕니다
- 짝수 인덱스: E[k]=x[2k]E[k] = x[2k] (k = 0, 1, …, N/2-1)
- 홀수 인덱스: O[k]=x[2k+1]O[k] = x[2k+1] (k = 0, 1, …, N/2-1)
- 작은 DFT 두 개 수행:
- EE에 대한 DFT 계산: DFT(E)=E[0],E[1],...,E[N/2−1]\text{DFT}(E) = E[0], E[1], ..., E[N/2-1]
- OO에 대한 DFT 계산: DFT(O)=O[0],O[1],...,O[N/2−1]\text{DFT}(O) = O[0], O[1], ..., O[N/2-1]
- 결과를 하나로 합침:
- DFT의 특성을 활용한 버터플라이 연산 수행
- 각 k에 대해 (k = 0, 1, …, N/2-1):
- X[k]=DFT(E)[k]+ωNk⋅DFT(O)[k]X[k] = \text{DFT}(E)[k] + \omega_N^k \cdot \text{DFT}(O)[k]
- X[k+N/2]=DFT(E)[k]−ωNk⋅DFT(O)[k]X[k+N/2] = \text{DFT}(E)[k] - \omega_N^k \cdot \text{DFT}(O)[k]
- 여기서 ωN=e−2πi/N\omega_N = e^{-2\pi i/N}은 회전 인자(twiddle factor)입니다
즉,
- 큰 문제를 절반 크기의 두 문제로 분할하여 해결
- 재귀적으로 반복하면서 문제 크기를 계속 줄임
- 전체 복잡도: O(NlogN)O(N \log N) (기존 DFT는 O(N2)O(N^2))
📊 시각화 예시 (길이 8 수열)
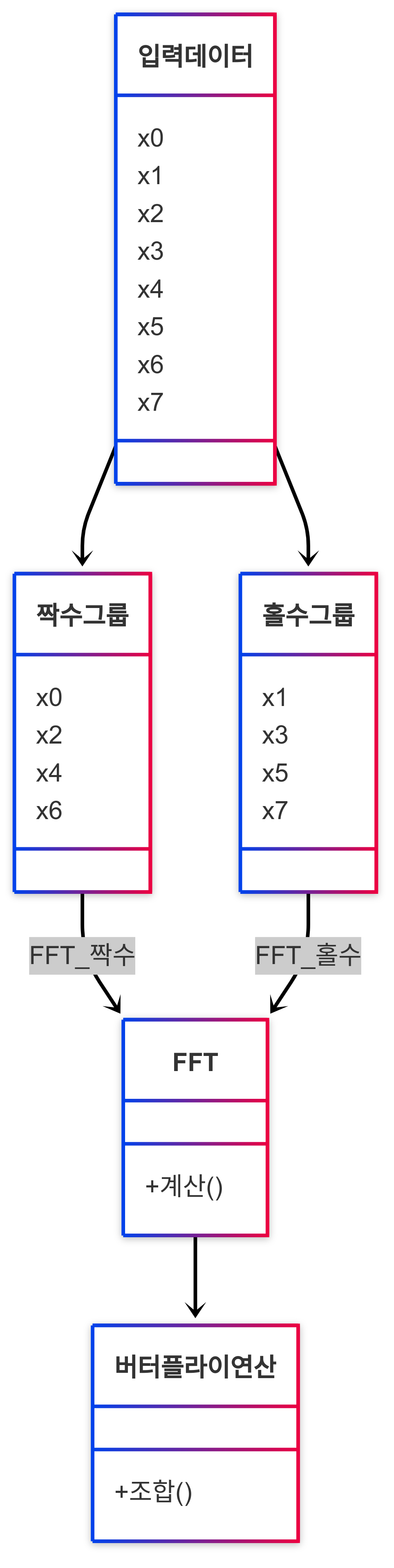

버터플라이 연산 시각화
DFT(Even)[k] ──┬─────► X[k]
│
⊕
│
DFT(Odd)[k] ───┼─┐
│ │
ωᴺᵏ│ │
│ │
└─⊕─► X[k+N/2]🔄 복소수 특성 활용
FFT의 효율성은 복소수의 특성을 활용하는 데서 비롯됩니다:
- 회전 인자(twiddle factor) ωNk\omega_N^k의 주기성 활용
- ωNk+N/2=−ωNk\omega_N^{k+N/2} = -\omega_N^k 특성 이용
- 대칭성을 통해 계산량 절감
회전 인자의 기하학적 의미
회전 인자 ωN=e−2πi/N\omega_N = e^{-2\pi i/N}는 복소 평면에서 단위원을 따라 NN등분하는 점들을 나타냅니다. 이는 각 주파수 성분이 신호에 기여하는 방식을 계산하는 데 활용됩니다.
✏️ 정리
구분
내용
입력
시간 영역 수열
출력
주파수 영역 (진동 패턴)
장점
컨볼루션을 빠르게 계산 가능
핵심
분할 정복 + 복소수 대칭성 활용
시간복잡도
O(NlogN)O(N \log N)
구현 난이도
중상 (복소수 연산 + 재귀적 구조)
메모리 요구
O(N)O(N)
✅ 실전 적용 요약
- 수열 A, B를 2의 거듭제곱 크기로 Zero Padding
- 예: 길이 5, 7인 수열을 길이 16(= 2⁴)으로 확장
- 확장된 부분은 0으로 채움
- FFT 수행 → 주파수 영역으로 변환
- A → FFT(A)
- B → FFT(B)
- 각 원소끼리 곱셈
- C[i] = FFT(A)[i] × FFT(B)[i]
- 역 FFT → 시간 영역으로 되돌림
- C → IFFT©
- 원하는 위치의 값 추출
- 결과는 IFFT©의 처음 (A의 길이 + B의 길이 - 1)개 원소
역 FFT (IFFT) 계산 방법
역 FFT는 기본적으로 FFT와 유사하지만 다음과 같은 차이가 있습니다:
- 회전 인자의 방향이 반대: ωN−k\omega_N^{-k} 대신 ωNk\omega_N^k 사용
- 결과를 N으로 나눔
🧾 요약 정리
개념
설명
예시
내적
같은 위치의 값끼리 곱하고 모두 더함
[1,2,3]·[4,5,6] = 1×4 + 2×5 + 3×6 = 32
순환 이동
끝을 앞으로 돌리는 연산
[1,2,3] → [3,1,2]
컨볼루션
두 수열을 겹치며 곱하고 더함
벨트에 스티커 붙이기 비유
FFT
빠르게 컨볼루션 계산하는 알고리즘
소리를 주파수로 나누는 것과 유사
다항식 곱셈
두 다항식 계수의 컨볼루션
(1+2x)(3+4x)=3+10x+8x2(1+2x)(3+4x) = 3 + 10x + 8x^2
💻 구현 예시 (Python)
📚 마무리 및 응용 분야
이 알고리즘은 단순한 수학 문제처럼 보이지만, 컴퓨터 과학에서 신호 처리에 널리 쓰이는 핵심 기술입니다:
- 멀티미디어 처리: 오디오 압축(MP3), 이미지 처리(JPEG), 비디오 코덱
- 통신 시스템: 변조/복조, 무선 통신, 5G 네트워크
- 과학 연구: 천체물리학, 양자 역학, 분자 동역학
- 의료 영상: MRI, CT 스캔 데이터 처리
- 머신러닝: 신경망의 컨볼루션 연산 가속화
FFT는 음악, 영상, 데이터 압축, 심지어 DNA 분석까지 폭넓게 활용되며, 이 알고리즘은 그 기초적인 아이디어를 응용한 좋은 예시입니다. 우리가 매일 사용하는 기술(이미지 처리, 음성 인식 등) 대부분이 이 원리를 응용하고 있습니다.
🔍 추가 학습 자료
- 푸리에 변환의 기하학적 이해
- 최적화된 FFT 구현 (비트 역전, 반복적 구현)
- 다차원 FFT와 응용
- 희소 FFT (Sparse FFT)와 근사 알고리즘
import sys
import math
import array
def fft_inplace(a_re, a_im, invert):
"""
a_re, a_im: array.array('d') 타입의 길이 n의 배열 (n은 2의 거듭제곱)
invert: False이면 FFT, True이면 역 FFT를 수행.
결과는 in-place로 a_re, a_im에 저장됨.
"""
n = len(a_re)
# memoryview로 빠른 인덱스 접근 (읽기/쓰기)
a_re_mv = memoryview(a_re)
a_im_mv = memoryview(a_im)
# 비트 반전 순서 재배열
j = 0
for i in range(1, n):
bit = n >> 1
while j & bit:
j -= bit
bit //= 2
j += bit
if i < j:
a_re_mv[i], a_re_mv[j] = a_re_mv[j], a_re_mv[i]
a_im_mv[i], a_im_mv[j] = a_im_mv[j], a_im_mv[i]
length = 2
while length <= n:
angle = 2 * math.pi / length * (-1 if invert else 1)
wlen_re = math.cos(angle)
wlen_im = math.sin(angle)
for i in range(0, n, length):
w_re = 1.0
w_im = 0.0
half = length >> 1
for j in range(i, i + half):
u_re = a_re_mv[j]
u_im = a_im_mv[j]
v_re = a_re_mv[j + half] * w_re - a_im_mv[j + half] * w_im
v_im = a_re_mv[j + half] * w_im + a_im_mv[j + half] * w_re
a_re_mv[j] = u_re + v_re
a_im_mv[j] = u_im + v_im
a_re_mv[j + half] = u_re - v_re
a_im_mv[j + half] = u_im - v_im
# w = w * (wlen_re + i*wlen_im)
temp_w_re = w_re * wlen_re - w_im * wlen_im
w_im = w_re * wlen_im + w_im * wlen_re
w_re = temp_w_re
length *= 2
if invert:
for i in range(n):
a_re_mv[i] /= n
a_im_mv[i] /= n
def convolution(a, b):
"""
a, b: 정수 리스트
두 리스트의 합성곱을 정수 리스트로 반환
"""
total_length = len(a) + len(b) - 1
n = 1
while n < total_length:
n *= 2
# a와 b를 array.array('d') 타입으로 만들고 0으로 패딩
A_re = array.array('d', a) + array.array('d', [0.0] * (n - len(a)))
A_im = array.array('d', [0.0] * n)
B_re = array.array('d', b) + array.array('d', [0.0] * (n - len(b)))
B_im = array.array('d', [0.0] * n)
fft_inplace(A_re, A_im, invert=False)
fft_inplace(B_re, B_im, invert=False)
# 두 FFT 결과를 원소별 곱셈 (복소수 곱셈)
for i in range(n):
temp_re = A_re[i] * B_re[i] - A_im[i] * B_im[i]
temp_im = A_re[i] * B_im[i] + A_im[i] * B_re[i]
A_re[i] = temp_re
A_im[i] = temp_im
fft_inplace(A_re, A_im, invert=True)
# A_re에 합성곱 결과가 저장되어 있음 (길이는 total_length)
result = [round(A_re[i]) for i in range(total_length)]
return result
def main():
data = sys.stdin.read().split()
if not data:
return
it = iter(data)
N = int(next(it))
X = [int(next(it)) for _ in range(N)]
Y = [int(next(it)) for _ in range(N)]
# X를 두 번 이어붙여 모든 순환 이동 고려 (길이 2N)
X_extended = X + X
# Y를 뒤집어서 합성곱을 통해 상관관계(내적) 계산
Y_rev = Y[::-1]
conv = convolution(X_extended, Y_rev)
# conv[k + (N-1)] = sum_{j=0}^{N-1} X_extended[k+j] * Y[j]
# k번째 순환 이동의 내적은 conv[N-1]부터 conv[2*N-1]에 있음 (총 N개)
best = 0
for i in range(N - 1, 2 * N - 1):
if conv[i] > best:
best = conv[i]
sys.stdout.write(str(best) + "\n")
if __name__ == '__main__':
main()
'Tech > Coding' 카테고리의 다른 글
| RSA 암호화 알고리즘의 원리와 예시 (0) | 2025.04.05 |
|---|---|
| PS(Problem Solving)에서의 컨볼루션과 컴퓨터 비전(CV, Computer Vision)에서의 컨볼루션 (0) | 2025.03.31 |
| Black and White Stones (0) | 2025.03.29 |
| 백준 28237번 문제 풀이 - 수학 선생님의 고민(Easy) (0) | 2025.03.27 |
| Python의 memoryview 객체 심층 분석 (0) | 2025.03.11 |



