백준4655🐨Hangover

https://www.acmicpc.net/problem/4655

Hangover (브론즈 III)

문제

어떻게 카드로 쌓아 만든 탑이 테이블을 얼마나 멀리까지 돌출하게 만들 수 있을까?
1장의 카드로는 최대 절반(1/2) 카드 길이만큼 돌출할 수 있다.
(카드는 테이블에 수직으로 세워진다고 가정한다.)
2장의 카드를 사용하면:

첫 번째 카드가 두 번째 카드 위로 1/2 길이만큼 돌출한다.
두 번째 카드가 테이블 위로 1/3 길이만큼 돌출한다.
총 돌출 길이는 ( 1/2 + 1/3 = 5/6 ) 카드 길이이다.

일반적으로 n장의 카드를 사용하면 ( 1/2 + 1/3 + 1/4 + … + 1/(n + 1) ) 카드 길이만큼 돌출할 수 있다.
위쪽 카드부터 두 번째 카드를 1/2, 두 번째 카드는 세 번째 카드 위로 1/3, 세 번째 카드는 네 번째 카드 위로 1/4의 길이만큼 돌출하게 쌓는다. 맨 아래의 카드는 테이블 위에서 1/(n + 1) 길이만큼 돌출된다. 아래 그림은 이 과정을 시각적으로 설명한다.

입력

여러 개의 테스트 케이스로 구성되며, 마지막에 0.00이 입력되면 입력이 종료된다.
각 테스트 케이스는 양의 실수 (c)가 주어지며, 최소 0.01에서 최대 5.20까지의 값을 가진다.
(c)는 소수 셋째 자리까지 제공된다.

출력

각 테스트 케이스에 대해, 주어진 돌출 길이 (c) 이상을 달성하기 위해 필요한 최소 카드 개수를 출력한다.
정확히 예제와 같은 형식으로 결과를 출력해야 한다.

예제 입력 1

1.00
3.71
0.04
5.19
0.00

예제 출력 1

3 card(s)
61 card(s)
1 card(s)
273 card(s)

풀이 아이디어

이 문제는 조화수(Harmonic Series, 역수가 등차수열, 각항은 0에 수렴하나 발산함.)와 관련된 문제로, (1/2 + 1/3 + 1/4 + …)의 형태로 누적된 값을 이용해 주어진 돌출 길이 (c)에 도달하는 최소 카드를 찾아야 한다.
유명한 리만 가설이랑 관련있다는...리만제타함수에 1을 대입하면 조화급수가 나온다고 한다.
$\zeta(1) = 1 + \frac{1}{2} + \frac{1}{3} + \cdots = \infty$
원래는 단순한 부루투포스 문제다. 그런데....요즘은 쉬운 문제를 어렵게 푸는게 재미있다.
어려운 문제는 어려워서 안 풀리니까...

구현 1

반복문을 이용해 (1/(i + 1)) 값을 계속 더해가면서 주어진 (c)를 넘을 때까지 반복한다.
이 과정에서 필요한 카드 수를 카운트해 출력한다.

*r,_=map(float,open(0).read().split())
for c in r:
    cards,cantilever = 0, 0.0
    while cantilever < c:
        cards += 1
        cantilever += 1 / (cards + 1)
    print(f"{cards} card(s)")

이렇게 구현하니까 바로 통과 되었다.
하지만 같은 연산을 반복한다는 생각이 들었다.
긴 길이를 잴 때 이미 더짧은 길이에 필요한 연산을 다 하니까
한 번 계산할 때 기록해두면 더 좋지 않을까?

구현 2

def s():
    *r, _ = map(float, open(0).read().split())
    max_value = max(r)
    dp, = [0.0]
    cantilever = 0.0
    cards = 0
    
    # max_value로 dp만들기
    while cantilever <= max_value:
        cards += 1
        cantilever += 1 / (cards + 1)
        dp.append(cantilever)
    
    # 카드 수 찾기 (이진 탐색 사용)
    for c in r:
        left, right = 0, len(dp) - 1
        while left < right:
            mid = (left + right) // 2
            if dp[mid] < c:
                left = mid + 1
            else:
                right = mid
        index = left
        print(f"{index} card(s)")
s()

최대값을 찾아서 dp를 만들고 dp를 이분탐색해서 카드의 수를 찾는다.
근데 뭔가 max를 찾느라 에너지를 한번 더 쓰는 느낌이라 다음 구현을 만들어 보았다.

구현3

*r, _ = map(float, open(0).read().split())
dp = [0.0]
cantilever = 0.0
cards = 0
max_value = 0.0

for c in r:
    if c > max_value:
        while cantilever <= c:
            cards += 1
            cantilever += 1 / (cards + 1)
            dp.append(cantilever)
        max_value = c
    
    left, right = 0, len(dp) - 1
    while left < right:
        mid = (left + right) // 2
        if dp[mid] < c:
            left = mid + 1
        else:
            right = mid
    index = left
    print(f"{index} card(s)")

최대값을 갱신하면서 최대값보다 큰 값이면 현재 길이보다 길어질때까지 연산하고 더 작은 값이면 이분탐색하는 방법을 구현했다.

구현 4

곰곰히 생각하니 이분탐색의 효용성이 좀 의구심이 가서 힙큐로 작은 값 부터 차례로 연산해서 중복 연산을 줄이려고 해 보았다.

def s():
    import heapq
    *r, _ = map(float, open(0).read().split())
    cantilever = 0.0
    cards = 0
    #우선순위 큐로 작은값부터 찾으면서 딕셔너리 기록
    r_heap = list(r)
    heapq.heapify(r_heap)
    results = {}
    while r_heap:
        c = heapq.heappop(r_heap)
        while cantilever < c:
            cards += 1
            cantilever += 1 / (cards + 1)
        results[c] = cards
    #원래 순서로 출력    
    open(1,'w').write('\n'.join(f"{results[c]} card(s)" for c in r))
s()

결과

결과는 좀 슬픈데 구현 1의 압도적인 승리다.(길이가 짧으니까.)

목표 숫자가 엄청 크면 좀 차이가 나지 않을까 생각해본다. 그리고 실험해보니 차이가 확실했다.
힙큐 방식으로 2초 이내에서는 길이 14~15정도까지 연산할 수 있는 것 같다.
그리고 특정 숫자는 연산량이 적다.

https://youtu.be/AeeE-RPmOWw

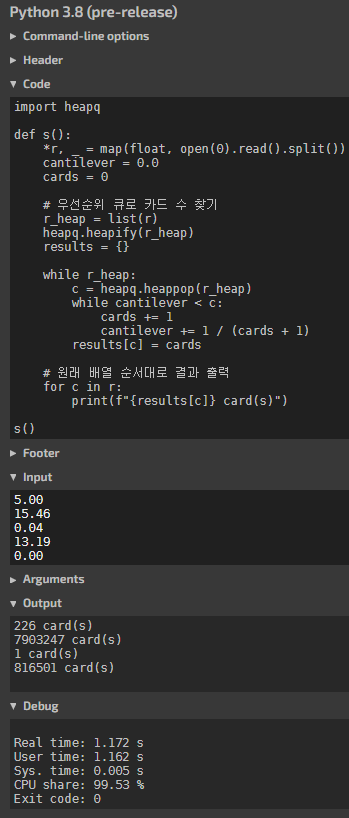
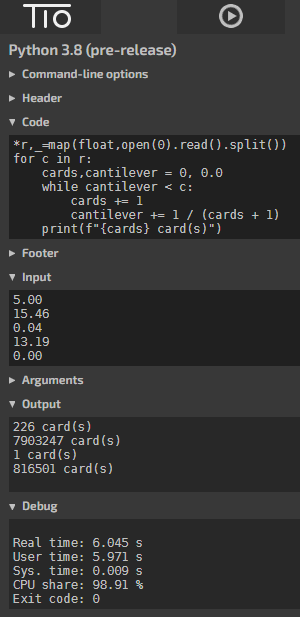
이 문제를 즐겁게 푼 이유중에 하나인데 이전에 긱블 동영상에서 같은 문제를 실제로 본 적이 있다.
긱블에서 계산기 엑셀파일까지 만들어서 공유해 두었다.

계산기 주소: https://cafe.naver.com/geekbleofficial/15891

여담으로 입출력시 새로운 방법을 쓰게 되었는데,
입력 끝에 0을 주는 문제는 0을 확인하거나 잘라내야 했다.

r=list(map(float,open(0).read().split()[:-1]))

그러면 리스트를 복사해서 생성하는 비용이 발생했다.

*r,_=map(float,open(0).read().split())

라고 해 버리면 맨 끝의 데이터 0을 잘라내고 쓸 수 있다.
0이 끝에 세 개 오면

*r ,_ ,_ ,_ =map(float,open(0).read().split())

하면 된다. 안 그러면 여기에 list를 씌우고 잘라내야 해서...불편하다(괄호가 많아지기도 하고)

추가

조화수 추정으로 풀 수도 있다. 1+1/2+...1/k의 합을 구하는 근사치 추정식이 있다.

0.5 1.45에서 오류가 나는데 이유를 모르겠다.(근사값 추정함수가 값이 충분히 크지 않아서 튀는 값인 듯)
어거지로 해당 값은 보정함.

import math

# 목표 값 입력
*targets, _ = map(float, open(0).read().split())

# 오일러-마스케로니 상수
gamma = 0.5772156649

for target in targets:
    # 목표 값을 1 증가시켜 근사값 추정 (1/2부터 시작)
    n_estimate = math.exp(target - gamma + 1)  
    n_approx = max(1,int(n_estimate)-2)#직전부터 확인

    # 1/2부터 n_approx까지의 조화수 합 계산
    harmonic_sum = sum(1 / k for k in range(2, n_approx + 1))

    # 근사된 n 직전부터 초과 지점 탐색
    k = n_approx + 1
    while harmonic_sum <= target:
        harmonic_sum += 1 / k
        k += 1
    print(f"{k - 2-(target in {1.45,0.5})} card(s)")

저작자표시 비영리 변경금지

붉은 각설탕