
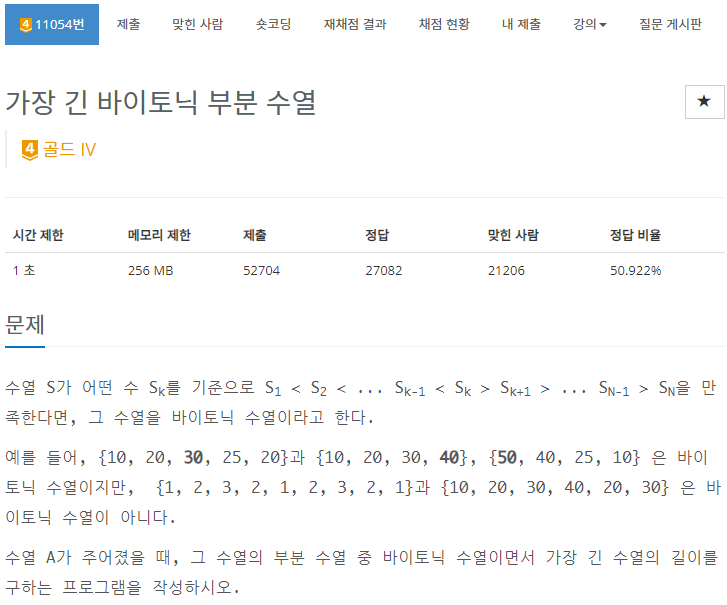

이번에는 글을 쓰면서 풀어 보자 . 이 문제는 최장 증가 수열 문제를 응용한 문제다. 그런데 최장 증가 수열 문제의 내 코드를 보아도 이해가 바로 안 가서 다시 공부했다.
먼저 LIS라고도 하는 최장 증가 수열 A에 대해 A[i]가 i번째 원소라고 하면 dp는 다음과 같이 정의할 수 있다.
dp[i] = i번째 원소를 포함하는 가장 긴 증가하는 수열
증가하는 수열이 i번째 수를 포함하려면 포함시키려는 기존 수열의 마지막 원소가 i번째 수보다 작아야 한다. 만약, i번째 수를 포함시킬 수 있다면( 기존 수열의 마지막 원소가 i번째 수보다 작다면) 기존 수열의 길이에 + 1을 하면 된다.
그러니까 dp[i]를 정할 때,
for i in range(n):
for j in range(i):
if a[i] > a[j]:
inc[i] = max(inc[i], inc[j]+1)와 같은 과정으로 할 수 있다.
이 코드의 의미는 i번째까지의 수열을 살펴보면서 만약 붙일 수 있는(a[i]보다 작은 원소인 a[j]) 위치면 기존 길이에 +1을 해 보면서 최대값을 기록하는 방법이다.
그런데 이 문제에서는 증가하는 길이와 감소하는 길이를 더해야 하기 때문에 위의 최장 증가 수열에 쓰인 dp를 2개 만들면 된다. 그리고 만들어진 dp를 더하고 최대값을 출력하면 가장 긴 바이토닉 부분 수열의 길이를 알 수 있다. 이때 1을 빼는 이유는 i번째 원소를 두 번 포함하기 때문이다.
n = int(input())
a = list(map(int, input().split()))
inc = [1 for i in range(n)]
dec = [1 for i in range(n)]
for i in range(n):
for j in range(i):
if a[i] > a[j]:
inc[i] = max(inc[i], inc[j]+1)
ir=-(i+1)
jr=-(j+1)
if a[ir] > a[jr]:
dec[ir] = max(dec[ir], dec[jr]+1)
dp = [inc[i] + dec[i] -1 for i in range(n)]
print(max(dp))https://youtu.be/K-F6ABsRV9M?si=lzs0gHNWnMEsi3X6
https://youtu.be/6QkmRvHMfqs?si=R0Qgpzbd8AmLaTje
https://youtu.be/aPQY__2H3tE?si=eaWwlI6kFqd7PHnc
'Tech > Coding' 카테고리의 다른 글
| 나의 방학 (0) | 2024.03.02 |
|---|---|
| 가장 가까운 두 점 (0) | 2024.03.02 |
| 1932번 정수 삼각형 (0) | 2024.02.28 |
| 1463번 1로 만들기 (0) | 2024.02.28 |
| 25494번 단순한 문제 (Small) (0) | 2024.02.27 |

