
동적 프로그래밍이 어려워서 한 문제씩 차근차근히 공부해 보기로 했다.

1. 문제의 이해
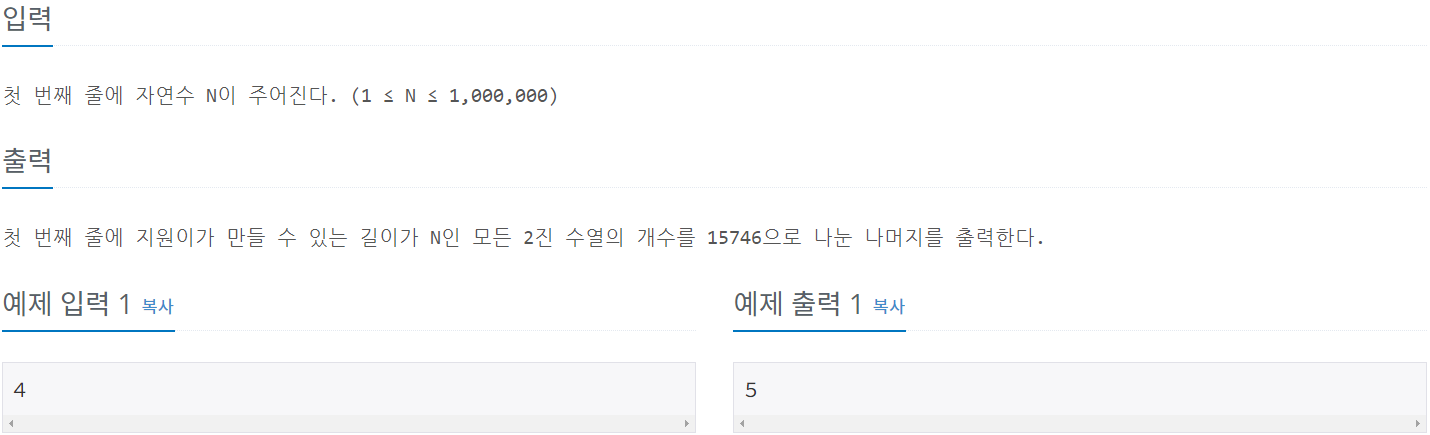
00이 쓰여진 타일과 1이 쓰여진 타일로 크기 N을 몇 가지 만들 수 있나? 라는 문제다.
문제를 단순화하면, 00은 길이2, 1은 길이1로 생각한다.
그러면 2와 1을 써서 만들 수 있는 합이 N나오는 순열 개수 구하기다.
길이가 1일 때 만들 수 있는 순열은 [1] 한 가지.
길이가 2일 때 만들 수 있는 순열은 [2]와 [1,1] 두 가지다.
2. dp의 정의
타일을 길이만큼 채워 나갈 때 공간이 점점 줄어들고, 그 과정에서 과거에 채워 본 공간이 계속 등장한다.
다시말해 과거의 연산을 이용해서 가짓수를 구할 수 있다.
길이 1과 2를 계산한 후 길이 3의 공간을 채운다고 했을 때, 길이 1짜리 타일을 붙이고 나면 2의 공간이 남는데 이미 길이 2일때의 경우의 수 값을 계산해서 알고 있다.
그렇다면 길이 1짜리를 붙였을 때 2가지, 길이 2짜리를 붙였을 때 1가지를 합치면 된다.
dp[i]를 i길이만큼 타일을 붙일 수 있는 경우의 수 라고 정의하고 문제를 풀면 된다.
3. 점화식
앞서 이야기한 대로 i 길이만큼의 타일부착 경우의 수는 i-1일때와 i-2일때의 합과 같다.
그러면 dp[i]=dp[i-1]+dp[i-2] 가 된다.
코드를 짜 보자.
def tile(N):
dp = [0,1,2]
if N < 3:
return dp[N]
dp += [0] * (N - 2)
for i in range(3, N + 1):
dp[i] = dp[i - 1] + dp[i - 2]
return dp[N]
print(tile(int(input())))결과는?

이전 결과를 모두 저장하는 게 문제인 것 같다.
그럼 덮어써야겠네..
def tile(N):
dp = [0,1,2,0]
if N < 3:
return dp[N]
for _ in range(3, N + 1):
dp[3] = dp[2] + dp[1]
dp.pop(0)
dp+=[0]
return dp[2]
print(tile(int(input())))
아놔! 진짜.
pop 이나 리스트 자체에서 시간 손해를 줄여보자.
def tile(N):
if N < 3:
return N
dp1, dp2 = 1, 2
for i in range(3, N + 1):
dp1, dp2 = dp2, dp1 + dp2
return dp2
print(tile(int(input())))리스트는 없앴지만 변수명에 미련이 남아 있다....

아;; 원인이 다른 데 있나보다....
분명 다이나믹이라고 되어 있는데 이쯤 되면 공식이 개입한다는 느낌이다.
[1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946]
이거 혹시....피보나치냐...
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597
그러니까 피보나치 N+2번째 수를 구하는거네...
피보나치 위키피디아에 가니 이런 그림이 있다.

어, 파도반 수열 할 때

이런 그림이 있었는데...
아무튼 이전에 푼 피보나치 문제들이 있으니 기억을 떠올려 보자.

이거 행렬로 풀었었는데;;
https://www.notion.so/1003-DP-MEMO-1348561a670d46c29753b6b256abd022?pvs=4
🙂#1003 DP, MEMO + 분할 정복 | Notion
와 피보나치다! CPP 코드도 줬네? 전역변수 써서 더하면 되잖아 하고 풀다가 뭔가 이상함을 감지했습니다. 게다가 라이브러리 문제로 컴파일 에러도 났습니다. 나중에 의도대로 수정해 보니 역시
atom-billboard-be7.notion.site
https://www.notion.so/11444-6-8cc5e06eefbc488aa304af5aa76ddd15?pvs=4
#11444번 피보나치 수 6 | Notion
문제
atom-billboard-be7.notion.site
https://www.notion.so/9c01cbf6b82b4c9bb7f927da83503575?pvs=4
🐨코알라 스터디🐨 | Notion
Built with Notion, the all-in-one connected workspace with publishing capabilities.
atom-billboard-be7.notion.site

한참을 보다 보니 싸한 느낌이 들었다. 수가 엄청 커지는데?


아.....나는 문제를 잘 안 읽는 스타일이다...
어제도 이랬다.(소수가 아닌 것인데 소수인 것 한 시간 찾음)
아무튼 저때 배운 것이 모드연산은 분배가 가능.
일단 피보나치 코드로 비정상적으로 어렵게 풀어보자.
def matrix_multiply(a, b):
return [[(a[0][0]*b[0][0] + a[0][1]*b[1][0])%15746, (a[0][0] * b[0][1] + a[0][1] * b[1][1])%15746],
[(a[1][0]*b[0][0] + a[1][1]*b[1][0]%15746), (a[1][0] * b[0][1] + a[1][1] * b[1][1])%15746]]
def matrix_power(matrix, n):
if n == 1:
return matrix
if n % 2 == 0:
half_power = matrix_power(matrix, n // 2)
return matrix_multiply(half_power, half_power)
else:
return matrix_multiply(matrix, matrix_power(matrix, n - 1))
def fibo(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
result_matrix = matrix_power([[1, 1], [1, 0]], n - 1)
return result_matrix[0][0]
n=int(input())
print(fibo(n+1))(7등의 속도가 나오는 행렬연산 코드..이 문제에 이런 짓 하는 사람이 많을 리가 없다.)

출제자가 의도한 코드도 만들어 보았다.
def tile(N):
if N < 3:
return N
dp1, dp2 = 1, 2
for i in range(3, N + 1):
dp1, dp2 = dp2, (dp1 + dp2)%15746
return dp2
print(tile(int(input())))
1등은 비트 연산과 행렬 곱셈을 사용하여 피보나치 수열을 빠르게 구하는 방법을 구현했다고 한다. 도저히 이해가 안 가서 gpt에게 물었다. 코드는 첨부하기는 좀 그렇다.
1. `m(a, b)` 함수는 두 행렬 `a`와 `b`의 곱을 계산합니다. 이는 행렬의 곱셈을 이용하여 구현되어 있습니다.
2. `s(a, n)` 함수는 입력값 `n`에 해당하는 피보나치 행렬의 거듭제곱을 구합니다. 이 함수는 입력값 `n`을 이진수로 변환하여, 각 자릿수에 해당하는 피보나치 행렬의 거듭제곱을 구하고, 이를 곱셈을 이용하여 결합합니다.
3. 마지막으로 `m(s([[1,1],[1,0]], int(input())+1), [[1],[0]])[1][0]`은 입력값에 해당하는 피보나치 수열의 값 중에서 두 번째 값을 출력합니다. 이는 피보나치 행렬의 거듭제곱을 구하고, 이 중에서 두 번째 행렬의 첫 번째 열의 값을 출력하는 것입니다.
위 코드는 피보나치 수열을 빠르게 구하는 방법 중 하나를 구현한 것이며, 입력값에 해당하는 피보나치 수를 15746으로 나눈 나머지를 출력합니다. 이렇게 나머지를 구하는 이유는 수가 커지면서 발생할 수 있는 오버플로우를 방지하기 위함입니다.
...더 모르겠다.
'Tech > Coding' 카테고리의 다른 글
| Embedding a Python Playground (0) | 2024.02.26 |
|---|---|
| # 20920번 영단어 암기는 괴로워 (0) | 2024.02.26 |
| 음? (0) | 2024.02.24 |
| 카데인 알고리즘(Kadane's Algorithm) (0) | 2024.02.24 |
| RGB거리 (0) | 2024.02.22 |


