https://www.acmicpc.net/problem/29358
를번역한 문제다.
| 시간 제한 | 메모리 제한 |
|---|---|
| 2 초 | 1024 MB |
문제
로키가 헐크를 잡으려 할 때, 자신의 힘을 조금 잘못 계산하여 실수로 헐크를 평행한 \(n\)차원 세계로 보내버렸다. 그 후 로키는 헐크를 얼음 덩어리 속에 완전히 얼려버렸다. 최종적인 승리를 위해 로키는 얼음 덩어리에서 불필요한 얼음을 잘라내어 얼어붙은 헐크만 남기면 된다.
로키가 모든 일을 옮겨간 공간은 최대 3차원이다. 1차원 공간에서 얼음 덩어리는 어떤 길이의 선분이고, 그 안의 헐크는 그 안에 포함된 선분이다. 2차원 공간에서 얼음 덩어리와 헐크는 좌표축에 평행한 변을 가진 직사각형이며, 헐크는 얼음 덩어리 안에 포함되어 있다. 마찬가지로, 3차원 공간에서 얼음 덩어리와 헐크는 좌표축에 평행한 변을 가진 직육면체이다.
로키는 얼음 덩어리에서 일부 얼음 조각을 잘라낼 수 있다. 1차원 공간에서 절단은 점이고, 2차원에서는 직선이며, 3차원에서는 평면이다. 어떤 공간에서든 절단은 헐크를 통과해서는 안 되지만, 헐크에 접할 수는 있다. 로키는 얼음 덩어리에서 헐크가 있는 부분만 남기기 위해 최소 몇 번의 절단이 필요한지 알고 싶어한다.
입력
입력의 첫째 줄에는 하나의 정수 \(n\) (\(1 \le n \le 3\))이 주어진다 — 사건이 일어나는 공간의 차원 수이다.
다음 줄에는 \(n\)개의 자연수 \(a_i\) (\(1 \le a_i \le 10000\))가 주어진다 — 얼음 덩어리의 한 꼭짓점의 좌표이다. 이 꼭짓점의 반대편 꼭짓점은 원점에 있다고 가정한다.
다음 줄에는 먼저 \(n\)개의 정수 \(b_i\) (\(0 \le b_i \le a_i\))가 나열된다 — 헐크의 한 꼭짓점의 좌표이고, 그 다음 \(n\)개의 정수 \(c_i\) (\(0 \le c_i \le a_i\))가 나열된다 — 헐크의 반대편 꼭짓점의 좌표이다.
출력
로키가 헐크를 잘라내기 위해 필요한 최소 절단 횟수를 하나의 정수로 출력한다.
예제
예제 입력 1
1
5
0 3
예제 출력 1
1
예제 입력 2
2
3 4
2 2 3 3
예제 출력 2
3
예제 입력 3
3
2 2 2
0 1 0 1 2 1
예제 출력 3
3
언뜻 이해가 안 가서 그림으로 그려보니 의외로 간단했다.


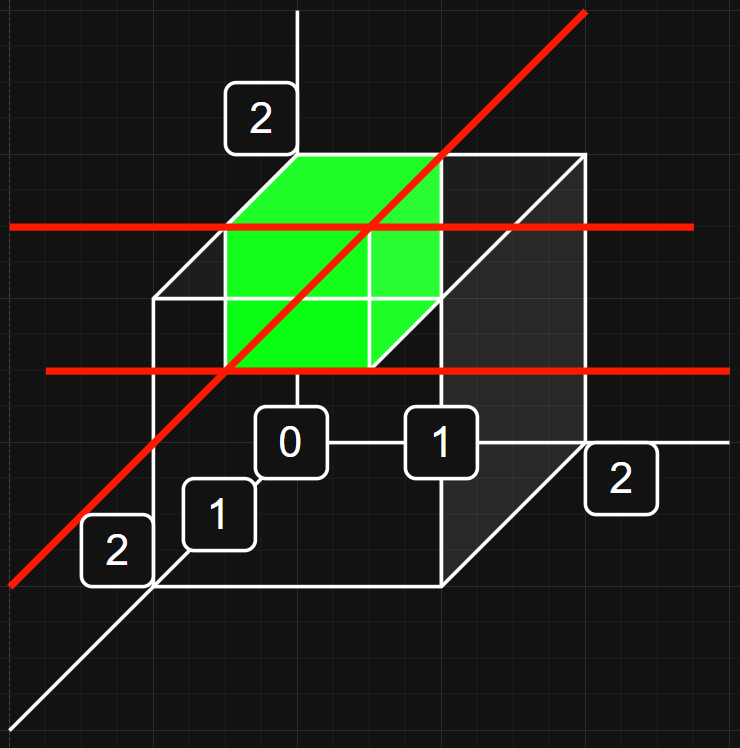
결국 각 차원에서 헐크의 시작 좌표가 0이 아니면 1번 추가, 끝 좌표가 해당 차원의 최대값이 아니면 또 1번 추가.
만약 두 좌표가 같으면 1번 감소가 되겠다.
a=map(int,open(0).read().split())
dim=next(a)
ends=[next(a) for _ in range(dim)]
p=list(a)
r=0
for i in range(dim):
r+=(p[i]!=0)+(p[i+dim]!=ends[i])-(p[i]==p[i+dim])
print(r)