순열 사이클 분할:백준 25577, 7805, 10451

1. 기본 개념

순열 $(a_1, a_2, \dots, a_n)$이 주어졌을 때, 이를 함수 $f(i)$로 표현할 수 있다. 여기서 $f(i)$는 $i$번째 원소를 다른 원소의 위치로 매핑하는 함수이다.

예를 들어, 순열 $(2, 3, 1)$이 있다면:

• $f(1) = 2$: 첫 번째 위치의 원소는 두 번째 위치로 간다.
• $f(2) = 3$: 두 번째 위치의 원소는 세 번째 위치로 간다.
• $f(3) = 1$: 세 번째 위치의 원소는 첫 번째 위치로 간다.

2. 함수의 반복적 적용

• $f^2(i) = f(f(i))$: 함수 $f$를 두 번 적용한 결과이다.
• $f^k(i)$: $f$를 $k$번 반복 적용한 결과이다.

만약 $i = f^k(i)$가 되는 최소 $k$를 찾으면, 이는 $i$가 순환하는 주기이다.

3. 순열 사이클

$i$에서 시작하여 $f$를 반복 적용하면 $ (f(i), f^2(i), \dots, f^k(i)) $라는 값들의 순환이 발생한다. 이를 순열 사이클이라고 한다. 같은 순열 사이클 안의 원소들은 모두 서로에게 연결되어 있다.

4. 순열 사이클 분할

순열의 모든 원소에 대해 순열 사이클을 구하면, 순열을 여러 개의 순열 사이클로 나눌 수 있다. 이를 순열 사이클 분할이라고 한다.

---

예시

예제 순열1: $(4, 3, 2, 1)$

• $f(1) = 4$
• $f(2) = 3$
• $f(3) = 2$
• $f(4) = 1$

순열 사이클 계산

1. $i = 1$부터 시작:
   • $f(1) = 4$
   • $f^2(1) = f(4) = 1$
     순열 사이클: $(1, 4)$
2. $i = 2$부터 시작:
   • $f(2) = 3$
   • $f^2(2) = f(3) = 2$
     순열 사이클: $(2, 3)$

순열 사이클 분할 결과

$(1, 4)$와 $(2, 3)$이라는 두 개의 순열 사이클로 분할된다.

---

예제 순열2: $(2, 1, 4, 3)$

1. $i = 1$부터 시작:
   • $f(1) = 2$
   • $f^2(1) = f(2) = 1$
     순열 사이클: $(1, 2)$
2. $i = 3$부터 시작:
   • $f(3) = 4$
   • $f^2(3) = f(4) = 3$
     순열 사이클: $(3, 4)$

순열 사이클 분할 결과

$(1, 2))와 ((3, 4)$이라는 두 개의 순열 사이클로 분할된다.

---

요약

• 주어진 순열에서 $f(i)$를 정의하고, 반복적으로 적용하여 $i = f^k(i)$가 되는 최소 $k$를 찾는다.
• 모든 원소를 확인하며 순열 사이클을 찾는다.
• 순열을 순열 사이클들로 나누는 과정을 순열 사이클 분할이라고 한다.
  
  

 

 

---

순열 사이클 분할 활용

1. 배열 정렬에서의 최소 스왑 계산

• 활용: 배열을 정렬하는 데 필요한 최소 교환 횟수 계산.
• 문제: 배열 [4, 3, 2, 1]을 오름차순으로 정렬하기 위해 필요한 최소 스왑 횟수를 구하라.
• 풀이:
  1. 각 숫자의 위치를 기준으로 순열을 작성: $(1 \to 4, 2 \to 3, 3 \to 2, 4 \to 1)$.
  2. 순열을 사이클로 분해: $(1, 4), (2, 3)$.
  3. 각 사이클의 길이에서 1을 뺀 값을 더해 스왑 횟수 계산: $(2-1) + (2-1) = 2$.

2. 고정점 없는 순열(Derangement) 계산

• 활용: 특정 조건을 만족하는 순열의 개수 계산.
• 문제: $n = 4$일 때, 고정점(fixed point)이 없는 순열의 개수를 구하라.
• 풀이:
  1. 고정점이 없는 순열은 모든 수가 자기 자신 외의 위치에 있어야 한다.
  2. 포함-배제 원리를 사용:
     $$D(n) = n! \left( 1 - \frac{1}{1!} + \frac{1}{2!} - \frac{1}{3!} + \cdots + \frac{(-1)^n}{n!} \right)$$
  3. $n = 4$일 때 $D(4) = 9$.

3. 그래프 연결 요소 분석

• 활용: 그래프의 연결 요소를 통해 문제 해결.
• 문제: $n = 6$이고 순열 $[4, 5, 6, 1, 2, 3]$이 주어질 때, 몇 개의 연결 요소로 나뉘는지 구하라.
• 풀이:
  1. 순열을 그래프의 간선으로 표현: $1 \to 4, 2 \to 5, 3 \to 6, 4 \to 1, 5 \to 2, 6 \to 3$.
  2. 사이클 분해: $(1, 4), (2, 5), (3, 6)$.
  3. 연결 요소 개수는 사이클 개수와 동일하므로 답은 $3$.

4. 암호학에서의 주기 분석

• 활용: 암호 키의 반복 주기 계산.
• 문제: 순열 $[3, 1, 4, 2]$의 주기를 계산하라.
• 풀이:
  1. 사이클 분해: $(1, 3, 4, 2)$.
  2. 사이클 길이 $4$가 주기이므로 답은 $4$.
     
     

관련 문제

백준25577🐨열정 정렬 정

열정이 가득한 김정렬은 항상 배열을 오름차순 정렬하려고 하는 강박증이 있습니다.
하지만 너무 열정적으로 정렬한 나머지 제대로 정렬하지 못하는 경우가 생깁니다.
김정렬의 친구로서, 정렬이가 눈치채기 전에 다시 정렬시켜주려고 합니다. 하지만 배열을 너무 많이 바꿀 경우 정렬이가 눈치를 채게 되고, 정렬이는 낙담할 것입니다.
우리가 배열에 적용할 수 있는 연산은 임의의 두 값을 뽑아서 서로 교환하는 것입니다. 정렬이 몰래 정렬하기 위해 최소한으로 필요한 연산 횟수를 구하세요.

입력

첫 번째 줄에 배열의 크기 $N (4 \leq N \leq 100,000)$이 주어집니다.
그다음 줄에 배열의 원소 $A_1, A_2, \cdots, A_n (-10^9 \leq A_i \leq 10^9, i \neq j \Rightarrow A_i \neq A_j)$이 주어집니다.
배열의 원소는 모두 정수입니다.

출력

배열에 적용할 최소 연산 횟수를 출력합니다.

예제 입력/출력

5
1 3 2 5 4

2

7
1 300 2 9012 3 400 0

4

15
86 30 24 13 82 62 85 27 11 55 97 39 81 41 63

13

---

def s():
    n,*a= map(int,open(0).read().split())
    b=sorted(a)
    pos = {val: i for i, val in enumerate(b)}
    c,v = 0,[1]*n
    for i in range(n):
        if a[i] != b[i] and v[i]:
            idx = i
            v[idx] = 0
            while a[idx] != b[i]:
                idx = pos[a[idx]]
                c += 1
                v[idx] = 0
    print(c)
s()

---

백준7805🐨최소 교환 (Minimum Swap)

실생활에서 순서를 오름차순 또는 내림차순으로 정렬하는 것은 흔한 문제입니다.
정렬 알고리즘에서 가장 일반적인 방법 중 하나는 두 원소를 비교하고 교환하는 것입니다. 새로운 정렬 알고리즘을 발명했다고 가정했을 때, 이 알고리즘에서 발생한 교환 횟수를 실제로 필요한 최소 교환 횟수와 비교하고 싶습니다.
주어진 문자 시퀀스를 오름차순으로 정렬하기 위해 필요한 최소 교환 횟수를 구하세요. 이 문제에서는 각 문자가 시퀀스에서 한 번만 등장한다고 가정합니다.

입력

각 줄에는 소문자로 이루어진 문자 시퀀스 $S (1 \leq |S| \leq 26)$가 주어집니다. $S$에 중복 문자는 없으며, 각 $i$번째 문자($0 < i < |S|$)는 'a'부터 'z' 사이의 문자입니다. 입력은 EOF로 종료됩니다.

출력

각 테스트 케이스에 대해, 문자를 오름차순으로 정렬하기 위해 필요한 최소 교환 횟수를 한 줄에 출력합니다.

예제 입력/출력

abc
cba
acb
bdca
fedcba

0
1
1
2
3

---

def s():
    res=[]
    for a in open(0,'rb'):
        a=a.rstrip()
        b=sorted(a)
        n=len(a)
        pos = {val: i for i, val in enumerate(b)}
        c,v = 0,[1]*n
        for i in range(n):
            if a[i] != b[i] and v[i]:
                idx = i
                v[idx] = 0
                while a[idx] != b[i]:
                    idx = pos[a[idx]]
                    c += 1
                    v[idx] = 0
        res.append(f"{c}")
    print('\n'.join(res))
s()

---

백준10451🐨순열 사이클

1부터 $N$까지 정수 $N$개로 이루어진 순열을 나타내는 방법은 여러 가지가 있습니다. 예를 들어, 8개의 수로 이루어진 순열 (3, 2, 7, 8, 1, 4, 5, 6)을 배열로 표현하면 아래와 같습니다.

$$ \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ 3 & 2 & 7 & 8 & 1 & 4 & 5 & 6 \end{pmatrix} $$

또는, Figure 1과 같이 방향 그래프로도 나타낼 수 있습니다.

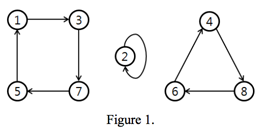
순열을 배열로 아래와 같이 나타냈다면:

$$ \begin{pmatrix} 1 & \dots & i & \dots & n \\ \pi_1 & \dots & \pi_i & \dots & \pi_n \end{pmatrix} $$

$i$에서 $\pi_i$로 간선을 이어 그래프로 만들 수 있습니다.

위 예시에서 (3, 2, 7, 8, 1, 4, 5, 6)으로 이루어진 순열 그래프에는 총 3개의 사이클이 존재합니다. 이러한 사이클을 "순열 사이클"이라고 합니다.

$N$개의 정수로 이루어진 순열이 주어졌을 때, 순열 사이클의 개수를 구하는 프로그램을 작성하세요.

입력

첫째 줄에 테스트 케이스의 개수 $T$가 주어집니다. 각 테스트 케이스의 첫째 줄에는 순열의 크기 $N$ ($2 \leq N \leq 1,000$)이 주어집니다. 둘째 줄에는 순열이 주어지며, 각 정수는 공백으로 구분되어 있습니다.

출력

각 테스트 케이스마다 입력으로 주어진 순열에 존재하는 순열 사이클의 개수를 출력합니다.

예제 입력/출력

2
8
3 2 7 8 1 4 5 6
10
2 1 3 4 5 6 7 9 10 8

3
7

 

---

def s():
    r=iter(map(int,open(0).read().split()))
    for _ in range(next(r)):
        n=next(r)
        a=[next(r) for _ in range(n)]
        cycle=0
        v=[True]*n
        for i in range(n):
            if v[i]:
                cycle+=1
                if i+1!=a[i]:
                    idx = i
                    v[idx]=False
                    while a[idx]!=i+1:
                        idx=a[idx]-1
                        v[idx]=False
        print(cycle)
s()

백준 문제 세트: https://www.acmicpc.net/problemset?sort=ac_desc&algo=171

솔브닥 세트: https://solved.ac/problems/tags/permutation_cycle_decomposition