🐨BOJ#1300] K번째 수

https://www.acmicpc.net/problem/1300

 

아이디어1 (구현+약간의 최적화)

n × n크기의 배열을 생성해서 일렬로 만든 뒤 개수를 Counter라이브러리로 세어서 키를 정렬해서 탐색

아이디어2 (약간의 최적화)

n × n크기의 배열을 처음부터 일렬로 만든 뒤 개수를 Counter라이브러리로 세어서 키를 정렬해서 탐색

from collections import Counter
n = int(input())
k = int(input())
c = Counter([i*j for i in range(1, n+1) for j in range(1, n+1)])

tot = 0
for key in sorted(c.keys()):
    tot += c[key]

    if tot >= k:
        print(key)
        break

결과: 메모리 초과가 나왔다. 4바이트 $10^{10}$개를 저장하기 위해서는 $4 \times 10^{10}\ $ 바이트 약 37.25 GB가 필요하다 ㅠㅠ

아이디어 3 -배열 관찰하기- 반비례 곡선

배열을 관찰해보면 특정 숫자 $t$ 이하의 숫자의 개수가 반비례 곡선에 의해 결정됨을 알 수 있다.
18 × 18의 배열에서 16이하의 숫자의 개수를 세는 방법은
첫줄에 16//1개, 둘째줄엔 16//2개, 3째 줄엔 16//3개 ...i번째 줄엔 16//i개로 $t$번의 순회로 특정 숫자 이하의 수 개수를 알 수 있다. 이 규칙을 이용하여 함수를 만들고 이 함수에 1~(n × n)의 숫자 사이에서 이분탐색을 하면 k번째 수가 어떤 수인지 알 수 있다.

def count_less_equal(x, n):
    count = 0
    for i in range(1, n+1):
        count += min(x // i, n)
    return count

def find_kth_smallest(n, k):
    low, high = 1, n * n
    while low < high:
        mid = (low + high) // 2
        if count_less_equal(mid, n) < k:
            low = mid + 1
        else:
            high = mid
    return low

# 입력 받기
n = int(input())
k = int(input())

# k번째 수 찾기
result = find_kth_smallest(n, k)
print(result)

아이디어 4 성능 개선- 곡선의 대칭성 이용하기 

그림을 살펴보면 곡선이 제곱수를 기준으로 선대칭이기 때문에
제곱수를 나타낸 선을 기준으로 탐색하면 계산을 위한 반복 횟수를 줄일 수 있다.
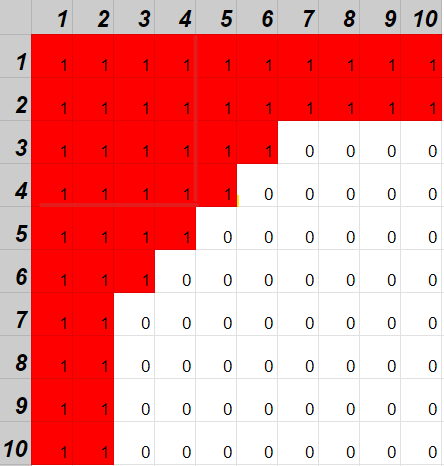
아래는 10×10의 배열에서 20이하의 숫자의 위치다.
4째 줄까지의 모양이 90도로 겹쳐 있다고 볼 수 있으므로 4줄만 계산하면 전체 넓이를 알 수 있다.
구체적으로는 타겟 숫자인 $t$이하의 숫자 개수를 셀 때int($\sqrt{t}$)개의 줄만 계산하면 개수를 알 수 있다.
구체적으로는 (1~4행에서 센 개수) × 2 - (겹치는 $4^2$개)
제곱을 따로 계산해도 되지만 매 행을 2배하고 int($\sqrt{t}$)씩  빼도 된다. 시간 차이는 나지 않았다.

def count_less_equal(i, n):
    count = 0
    sq = int(i**0.5)
    for j in range(1,sq+1):
        count+=min(i//j,n)*2-sq
    return count

def find_kth_smallest(n, k):
    low, high = 1, n * n
    while low < high:
        mid = (low + high) // 2
        if count_less_equal(mid, n) < k:
            low = mid + 1
        else:
            high = mid
    return low

# 입력 받기
n = int(input())
k = int(input())

# k번째 수 찾기
result = find_kth_smallest(n, k)
print(result)

파이파이 1등!  파이썬에서 나보다 빠른 알고리즘들이 파이파이를 안 써서 :)

 

파이썬 10위권!