https://namu.wiki/w/%EB%B6%84%ED%95%A0%20%EC%A0%95%EB%B3%B5%20%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
분할 정복 알고리즘
분할 정복(Divide and Conquer)은 여러 알고리즘의 기본이 되는 해결방법으로, 기본적으로는 엄청나게 크
namu.wiki
분할 정복 알고리즘 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 분할 정복 알고리즘(Divide and conquer algorithm)은 그대로 해결할 수 없는 문제를 작은 문제로 분할하여 문제를 해결하는 방법이나 알고리즘이다. 빠른 정렬이나 합
ko.wikipedia.org
분할 정복 알고리즘(Divide and conquer algorithm)
문제를 작게 분할해 해결한다. 퀵 정렬, 병합 정렬, 고속 푸리에 변환(FFT) 이 대표적이다. 보통 재귀로 구현한다.
function F(x):
if F(x)의 문제가 간단 then:
return F(x)을 직접 계산한 값
else:
x를 y1, y2로 분할
F(y1)과 F(y2)를 호출
return F(y1), F(y2)로부터 F(x)를 구한 값작은 부문제로 분할할 경우에 부문제를 푸는 알고리즘은 임의로 선택할 수 있다.
이러한 재귀호출을 사용한 함수는 함수 호출 오버헤드 때문에 실행 속도가 늦어진다.
빠른 실행이나 부문제 해결 순서 선택을 위해, 재귀호출을 사용하지 않고
스택, 큐(queue) 등의 자료구조를 이용하여 분할 정복법을 구현하는 것도 가능하다.
https://www.acmicpc.net/problem/2630
2630번: 색종이 만들기
첫째 줄에는 전체 종이의 한 변의 길이 N이 주어져 있다. N은 2, 4, 8, 16, 32, 64, 128 중 하나이다. 색종이의 각 가로줄의 정사각형칸들의 색이 윗줄부터 차례로 둘째 줄부터 마지막 줄까지 주어진다.
www.acmicpc.net


재귀 코드
def quad(x, y, N, paper):
color = paper[x][y]
for i in range(x, x+N):
for j in range(y, y+N):
if color != paper[i][j]:
# 4분할 탐색의 결과를 각각 계산
parts = [quad(x, y, N//2, paper), quad(x, y+N//2, N//2, paper),
quad(x+N//2, y, N//2, paper), quad(x+N//2, y+N//2, N//2, paper)]
# 각 부분의 결과를 합쳐서 반환
return [sum(x) for x in zip(*parts)]
# 모두 같은 색상이라면 해당 색상의 개수를 반환
return [0, 1] if color == 1 else [1, 0]
N = int(input())
paper = [list(map(int, input().split())) for _ in range(N)]
result = quad(0, 0, N, paper)
print(result[0]) # 0의 개수
print(result[1]) # 1의 개수반복문(스택)
N = int(input())
paper = [list(map(int, input().split())) for _ in range(N)]
# 영역을 나타내는 클래스 정의
class Area:
def __init__(self, x, y, size):
self.x = x
self.y = y
self.size = size
# 영역 검사 함수
def check_area(area, paper):
initial = paper[area.x][area.y]
for i in range(area.x, area.x + area.size):
for j in range(area.y, area.y + area.size):
if paper[i][j] != initial:
return False
return True
# 영역 분할 함수
def divide_area(area):
new_size = area.size // 2
return [Area(area.x, area.y, new_size), Area(area.x, area.y + new_size, new_size),
Area(area.x + new_size, area.y, new_size), Area(area.x + new_size, area.y + new_size, new_size)]
# 초기 영역 설정
areas = [Area(0, 0, N)]
white = 0
blue = 0
while areas:
current_area = areas.pop()
if check_area(current_area, paper):
if paper[current_area.x][current_area.y] == 0:
white += 1
else:
blue += 1
else:
areas.extend(divide_area(current_area))
print(white)
print(blue)
https://www.acmicpc.net/problem/1780
1780번: 종이의 개수
N×N크기의 행렬로 표현되는 종이가 있다. 종이의 각 칸에는 -1, 0, 1 중 하나가 저장되어 있다. 우리는 이 행렬을 다음과 같은 규칙에 따라 적절한 크기로 자르려고 한다. 만약 종이가 모두 같은 수
www.acmicpc.net
def novem(x, y, N, paper):
color = paper[x][y]
for i in range(x, x + N):
for j in range(y, y + N):
if color != paper[i][j]:
# 9분할 탐색의 결과를 각각 계산
parts = [
novem(x, y, N // 3, paper),
novem(x, y + 2 * N // 3, N // 3, paper),
novem(x, y + N // 3, N // 3, paper),
novem(x + 2 * N // 3, y, N // 3, paper),
novem(x + 2 * N // 3, y + 2 * N // 3, N // 3, paper),
novem(x + 2 * N // 3, y + N // 3, N // 3, paper),
novem(x + N // 3, y, N // 3, paper),
novem(x + N // 3, y + 2 * N // 3, N // 3, paper),
novem(x + N // 3, y + N // 3, N // 3, paper)
]
# 각 부분의 결과를 합쳐서 반환
return [sum(x) for x in zip(*parts)]
# 모두 같은 색상이라면 해당 색상의 개수를 반환
if color == 1:
return [0, 1, 0]
elif color == 0:
return [1, 0, 0]
else:
return [0, 0, 1]
N = int(input())
paper = [list(map(int, input().split())) for _ in range(N)]
result = novem(0, 0, N, paper)
print(result[-1]) # -1의 개수
print(result[0]) # 0의 개수
print(result[1]) # 1의 개수
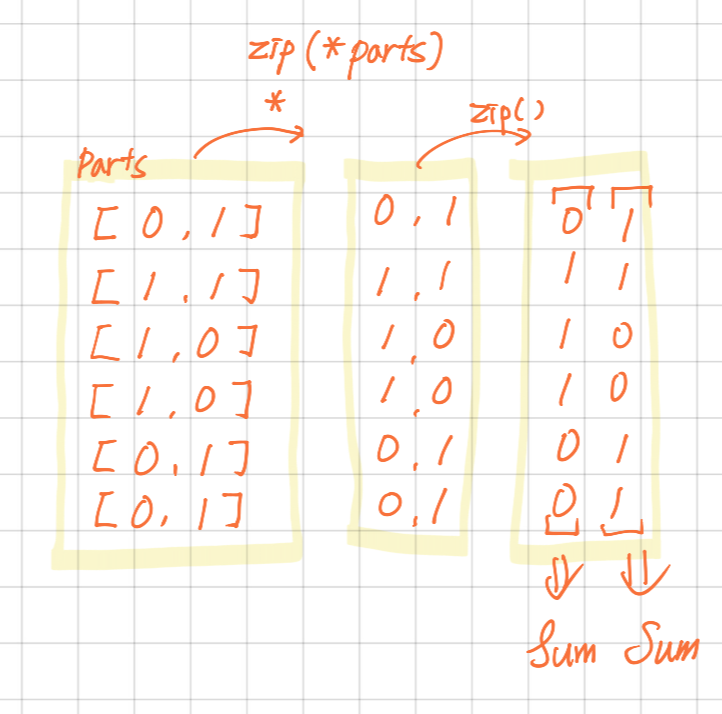
* 연산자와 zip() 함수는 파이썬에서 다양하게 사용됩니다. 두 기능을 함께 사용하면 특히 리스트나 튜플 같은 이터러블(iterable) 객체들을 다룰 때 유용합니다.
* 연산자
- 언패킹 용도: 컬렉션(리스트, 튜플 등)의 요소를 언패킹할 때 사용됩니다. 예를 들어, 함수에 여러 인자를 리스트 형태로 넘길 때 *를 사용하여 리스트의 각 요소를 개별 인자로 전달할 수 있습니다.
- 반복 확장: 리스트나 튜플을 반복 확장할 때 사용됩니다. 예를 들어, [1] * 3은 [1, 1, 1]을 생성합니다.
zip() 함수
- 이터러블 결합: 두 개 이상의 이터러블 객체를 인자로 받아, 각 객체의 동일 인덱스에 위치한 요소를 튜플로 묶어서 반환합니다. 결과는 zip 객체로 반환되며, 이는 list() 또는 tuple()로 변환하여 사용할 수 있습니다.
- 여러 시퀀스 동시 순회: 여러 리스트나 튜플을 동시에 순회하며, 각 리스트의 동일 위치에 있는 요소들을 처리할 때 유용합니다.
* 연산자와 zip() 함수의 결합 사용 예
* 연산자와 zip()을 함께 사용하면, 여러 리스트의 요소들을 "트랜스포즈(transpose)"할 수 있습니다. 즉, 행과 열을 바꾸는 작업입니다. 예를 들어, 두 리스트가 있을 때 각 리스트의 첫 번째 요소끼리, 두 번째 요소끼리 묶고 싶다면 다음과 같이 할 수 있습니다.
list1 = [1, 2, 3]
list2 = [4, 5, 6]
# zip과 * 연산자 사용
zipped = zip(list1, list2) # [(1, 4), (2, 5), (3, 6)]와 유사한 결과
transposed = zip(*zipped) # 원래 리스트로 되돌리기
# 결과 확인
list(transposed) # [(1, 2, 3), (4, 5, 6)]
이 예시에서 zip(*zipped)는 zip()에 의해 묶인 튜플들을 다시 원래의 리스트로 되돌리는 트랜스포즈(열과 행을 바꿈) 작업을 수행합니다. 이 기법은 행렬을 다룰 때 매우 유용합니다.
'Tech > Coding' 카테고리의 다른 글
| 🐨BOJ#1697 숨바꼭질]🙄BFS(feat. collections) (1) | 2024.03.29 |
|---|---|
| C언어 고급] 🚀배열과 포인터 (0) | 2024.03.28 |
| 🐨백준-파이썬]# 13305번 주유소(그리디 알고리즘) (0) | 2024.03.25 |
| 🐨백준 파이썬]# 1541번-잃어버린 괄호(그리디 알고리즘) (0) | 2024.03.24 |
| 🐨알고리즘] 비트 필드를 활용한 다이나믹 프로그래밍 (1) | 2024.03.24 |



